若关于x的不等式|ax+a+2|<2有且只有一个整数解,求a的整数值.
【答案】
分析:根据绝对值的意义,|ax+a+2|<2即可得到-2<ax+a+2<2,从而求得ax的范围是-a-4<ax<-a,然后分a>0和a<0两种情况讨论,即可求得不等式的解集,其中解集用a表示,根据不等式只有一个整数解,即可得到关于a的不等式,从而求得a的值.
解答:解:由题可得-a-4<ax<-a,
若a=0,则-4<0<0,不等式无解,不合题意舍去.
若a>0,则
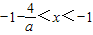
,
∵不等式有惟一整数解,
∴
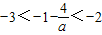
,即
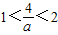
.
∴
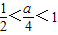
,即2<a<4,
∴整数a值只能为3.
若a<0则
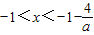
∵不等式有惟一整数解
∴
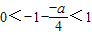
,即
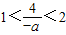
,
∴
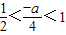
,即-4<a<-2,
∴整数a的值为-3.
综上所求,a的整数值为±3.
点评:本题主要考查了含有绝对值的不等式的解决方法,正确去掉绝对值符号是解题的关键.

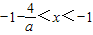 ,
,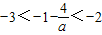 ,即
,即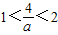 .
.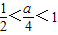 ,即2<a<4,
,即2<a<4,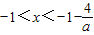
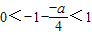 ,即
,即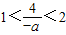 ,
,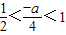 ,即-4<a<-2,
,即-4<a<-2,

 名校课堂系列答案
名校课堂系列答案