
| A. | 0 | B. | $\sqrt{3}$ | C. | -2 | D. | ±2 |
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省成都市金堂县八年级上学期期末考试数学试卷就(解析版) 题型:解答题
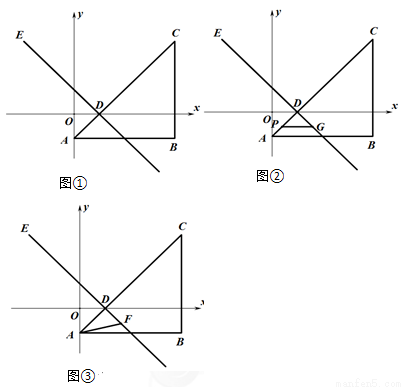
如图①,等腰直角三角形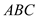 的顶点
的顶点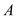 的坐标为
的坐标为 ,
,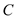 的坐标为
的坐标为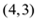 ,直角顶点
,直角顶点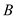 在第四象限,线段AC与x轴交于点D.将线段DC绕点D逆时针旋转90°至DE.
在第四象限,线段AC与x轴交于点D.将线段DC绕点D逆时针旋转90°至DE.
(1)直接写出点B、D、E的坐标并求出直线DE的解析式.
(2)如图②,点P以每秒1个单位的速度沿线段AC从点A运动到点C的过程中,过点P作与x轴平行的直线PG,交直线DE于点G,求与△DPG的面积S与运动时间t的函数关系式,并求出自变量t的取值范围.
(3)如图③,设点F为直线DE上的点,连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FE以每秒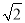 个单位的速度运动到E后停止.当点F的坐标是多少时,是否存在点M在整个运动过程中用时最少?若存在,请求出点F的坐标;若不存在,请说明理由.
个单位的速度运动到E后停止.当点F的坐标是多少时,是否存在点M在整个运动过程中用时最少?若存在,请求出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
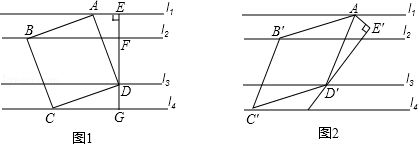
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
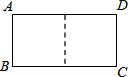 邻边不相等的矩形纸片,剪去一个最大的正方形,余下一个四边形,称为第一次操作,在余下的矩形纸片中再剪去一个最大的正方形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是正方形,则称原矩形为n阶方形,如图,矩形ABCD中,若AB=1,BC=2,则矩形ABCD为1阶方形.
邻边不相等的矩形纸片,剪去一个最大的正方形,余下一个四边形,称为第一次操作,在余下的矩形纸片中再剪去一个最大的正方形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是正方形,则称原矩形为n阶方形,如图,矩形ABCD中,若AB=1,BC=2,则矩形ABCD为1阶方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com