解:(1)∵AC平分∠BAD,CE⊥AB CF⊥AD,
∴CE=CF(角平分线上的点到角的两边的距离相等);
(2)全等.
理由如下:在Rt△BCE和Rt△DCF中,
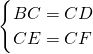
,
所以,Rt△BCE≌Rt△DCF(HL);
(3)在Rt△ACE中,∵AC=10,CE=6,
∴AE=

=

=8,
在Rt△ACE和Rt△ACF中,

,
∴Rt△ACE和Rt△ACF(HL),
∴AF=AE,
又∵AD=5,
∴DF=AF-AD=8-5=3;
(4)∵Rt△BCE≌Rt△DCF,
∴BE=DF,
∵Rt△ACE和Rt△ACF,
∴AE=AF,
∵AB=21,AD=9,
∴AD+DF=AB-BE,
即9+BE=21-BE,
解得BE=6,
在Rt△BCE中,CE=

=

=8,
又∵AE=AB-BE=21-6=15,
∴在Rt△ACE中,AC=

=
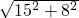
=17.
分析:(1)根据角平分线上的点到角的两边的距离相等解答即可;
(2)利用“HL”即可证明△BCE和△DCF全等;
(3)利用勾股定理列式求出AE的长度,然后利用“HL”证明△ACE和△ACF全等,根据全等三角形对应边相等可得AF=AE,再根据DF=AF-AD代入数据进行计算即可得解;
(4)根据全等三角形对应边相等可得BE=DF,然后求出BE的长度,然后求出AE,再根据勾股定理列式求出CE的长度,再利用勾股定理列式进行计算即可求出AC.
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,全等三角形的判定与性质,以及勾股定理的应用,比较简单,熟记性质是解题的关键.

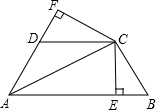 如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.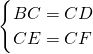 ,
, =
= =8,
=8, ,
, =
= =8,
=8, =
=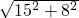 =17.
=17.

 名校课堂系列答案
名校课堂系列答案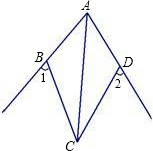

 如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.