
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
| n2+1 |
| n(n+1)(2n+1) |
| n2+1 |
| n(n+1)(2n+1) |

| OB |
| OC |
| AP |
| AB |
| CE |
| ED |
| a |
| a |
| a | ||
|
| 2 | ||
|
| 2a | ||
|
| 3a | ||
|
| 1 |
| 3 |
| n2+1 |
| n(n+1)(2n+1) |
 Ł¨1Ł©×÷PAˇÍyÖáÓÚAŁ¬ÍĽÖеġ°7ˇ±×ÖĐÎÓë×ř±ęÖáµÄ˝»µă·Ö±đÎŞBˇ˘Cˇ˘DŁ¬ČçÍĽ1Ł¬
Ł¨1Ł©×÷PAˇÍyÖáÓÚAŁ¬ÍĽÖеġ°7ˇ±×ÖĐÎÓë×ř±ęÖáµÄ˝»µă·Ö±đÎŞBˇ˘Cˇ˘DŁ¬ČçÍĽ1Ł¬| CE |
| OB |
| DE |
| OC |
| CE |
| AP |
| DE |
| AB |
| OB |
| OC |
| AP |
| AB |
| CE |
| ED |
| a |
| a |
| a | ||
|
| 2 | ||
|
| 3a | ||
|
| 2a | ||
|
| 3a | ||
|
| 2a | ||
|
| 3a | ||
|
| 1 |
| 3 |
| CE |
| OB |
| DE |
| OC |
| CE |
| AP |
| DE |
| AB |
| OB |
| OC |
| AP |
| AB |
| CE |
| ED |
| 2a |
| a |
| 2a | ||
|
| 3a | ||
|
| 6a | ||
|
| 5a | ||
|
| 6a | ||
|
| 5a | ||
|
| 6a | ||
|
| 5a | ||
|
| 5 |
| 30 |
| CE |
| OB |
| DE |
| OC |
| CE |
| AP |
| DE |
| AB |
| OB |
| OC |
| AP |
| AB |
| CE |
| ED |
| 3a |
| a |
| 10 |
| 84 |
| CE |
| OB |
| DE |
| OC |
| CE |
| AP |
| DE |
| AB |
| OB |
| OC |
| AP |
| AB |
| CE |
| ED |
| 4a |
| a |
| 17 |
| 180 |
| 1 |
| 3 |
| 2 |
| 2ˇÁ3 |
| 12+1 |
| 1ˇÁ(1+1)ˇÁ(2+1) |
| 5 |
| 30 |
| 5 |
| 6ˇÁ5 |
| 22+1 |
| 2ˇÁ(2+1)ˇÁ(2ˇÁ2+1) |
| 10 |
| 12ˇÁ7 |
| 32+1 |
| 3ˇÁ(3+1)(2ˇÁ3+1) |
| 17 |
| 180 |
| 17 |
| 4ˇÁ5ˇÁ9 |
| 42+1 |
| 4ˇÁ(4+1)(2ˇÁ4+1) |
| n2+1 |
| n(n+1)(2n+1) |
| 1 |
| 3 |
| n2+1 |
| n(n+1)(2n+1) |


 ł¬ÄÜѧµäÓ¦ÓĂĚâĚ⿨ϵÁĐ´đ°¸
ł¬ÄÜѧµäÓ¦ÓĂĚâĚ⿨ϵÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐżÎłĚ | Ä꼶 | łőÖĐżÎłĚ |
| ¸ßŇ» | ¸ßŇ»Ăâ·ŃżÎłĚÍĆĽöŁˇ | łőŇ» | łőŇ»Ăâ·ŃżÎłĚÍĆĽöŁˇ |
| ¸ß¶ţ | ¸ß¶ţĂâ·ŃżÎłĚÍĆĽöŁˇ | łő¶ţ | łő¶ţĂâ·ŃżÎłĚÍĆĽöŁˇ |
| ¸ßČý | ¸ßČýĂâ·ŃżÎłĚÍĆĽöŁˇ | łőČý | łőČýĂâ·ŃżÎłĚÍĆĽöŁˇ |
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş044

˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş˝â´đĚâ
 µÄÍĽĎóÉĎŁ¬Áíˇ°7ˇ±×ÖĐÎÓĐÁ˝¸ö¶ĄµăÂäÔÚxÖáÉĎŁ¬Ň»¸ö¶ĄµăÂäÔÚyÖáÉĎŁ®
µÄÍĽĎóÉĎŁ¬Áíˇ°7ˇ±×ÖĐÎÓĐÁ˝¸ö¶ĄµăÂäÔÚxÖáÉĎŁ¬Ň»¸ö¶ĄµăÂäÔÚyÖáÉĎŁ®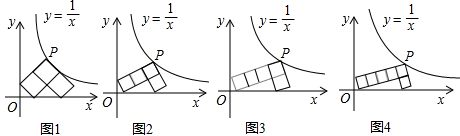
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş2013-2014ѧÄęËÄ´¨ĘˇłÉ¶ĽĘиßĐÂÇřľĹÄ꼶ÉĎѧĆÚĆÚÄ©żĽĘÔĘýѧĘÔľíŁ¨˝âÎö°ćŁ© ĚâĐÍŁşĚîżŐĚâ
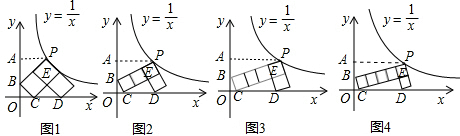
ČçÍĽ1ˇ«4ËůĘľŁ¬Ăż¸öÍĽÖеġ°7ˇ±×ÖĐÎĘÇÓÉČô¸É¸ö±ßł¤ĎŕµČµÄŐý·˝ĐÎĆ´˝Ó¶řłÉŁ¬ˇ°7ˇ±×ÖĐεÄŇ»¸ö¶Ąµă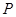 ÂäÔÚ·´±ČŔýşŻĘý
ÂäÔÚ·´±ČŔýşŻĘý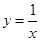 µÄÍĽĎńÉĎŁ¬Áíˇ°7ˇ±×ÖĐÎÓĐÁ˝¸ö¶ĄµăÂäÔÚ
µÄÍĽĎńÉĎŁ¬Áíˇ°7ˇ±×ÖĐÎÓĐÁ˝¸ö¶ĄµăÂäÔÚ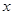 ÖáÉĎŁ¬Ň»¸ö¶ĄµăÂäÔÚ
ÖáÉĎŁ¬Ň»¸ö¶ĄµăÂäÔÚ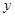 ÖáÉĎ.
ÖáÉĎ.
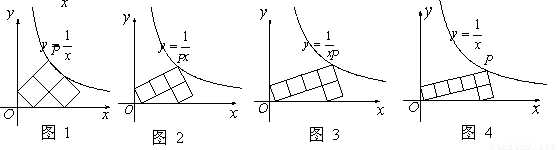
Ł¨1Ł©ÍĽ1ÖеÄÿһ¸öСŐý·˝ĐεÄĂć»ýĘÇ Ł»
Ł¨2Ł©°´ŐŐÍĽ1 ÍĽ2
ÍĽ2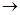 ÍĽ3
ÍĽ3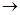 ÍĽ4
ÍĽ4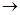
 ŐâŃůµÄąćÂÉĆ´˝ÓĎÂČĄŁ¬µÚ
ŐâŃůµÄąćÂÉĆ´˝ÓĎÂČĄŁ¬µÚ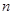 ¸öÍĽĐÎÖĐÿһ¸öСŐý·˝ĐεÄĂć»ýĘÇ
.Ł¨ÓĂş¬
¸öÍĽĐÎÖĐÿһ¸öСŐý·˝ĐεÄĂć»ýĘÇ
.Ł¨ÓĂş¬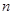 µÄ´úĘýĘ˝±íĘľŁ©
µÄ´úĘýĘ˝±íĘľŁ©
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łşşţ±±ĘˇÖĐżĽŐćĚâ ĚâĐÍŁş˝â´đĚâ
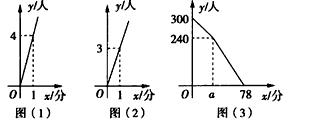
˛éż´´đ°¸şÍ˝âÎö>>
ąúĽĘѧУÓĹѡ - Á·Ď°˛áÁбí - ĘÔĚâÁбí
şţ±±Ęˇ»ĄÁŞÍřÎĄ·¨şÍ˛»ÁĽĐĹϢľŮ±¨Ć˝Ě¨ | ÍřÉĎÓĐş¦ĐĹϢľŮ±¨×¨Çř | µçĐĹթƾٱ¨×¨Çř | ÉćŔúĘ·ĐéÎŢÖ÷ŇĺÓĐş¦ĐĹϢľŮ±¨×¨Çř | ÉćĆóÇÖȨľŮ±¨×¨Çř
ÎĄ·¨şÍ˛»ÁĽĐĹϢľŮ±¨µç»°Łş027-86699610 ľŮ±¨ÓĘĎ䣺58377363@163.com