
已知A、B、C是半径为2的圆O上的三个点,其中点A是弧BC的中点,连接AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE.
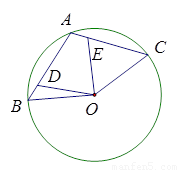
(1)求证:OD=OE;
(2)连接BC,当BC=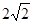 时,求∠DOE的度数.
时,求∠DOE的度数.
(1)详见解析;(2)∠DOE=45°.
【解析】
试题分析:(1)连接OA,可考虑证明△AOD≌△COE,有弧AB=弧AC,可得:∠AOB=∠AOC,在等腰⊿AOB和等腰⊿AOC中,两顶角相等,所以它们的底角也相等,从而可得:∠BAO=∠ACO ,再结合题中条件:OA=OC,AD=CE,根据“SAS”可证明△AOD≌△COE,从而得证.(2)如图2,根据垂径定理BF=CF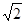 ,由勾股定理求得OF=
,由勾股定理求得OF=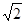 ,进而求得∠AOB=45°,由△AOD≌△COE,可得∠AOD=∠COE,再通过等量变换,即可求出∠DOE的度数.
,进而求得∠AOB=45°,由△AOD≌△COE,可得∠AOD=∠COE,再通过等量变换,即可求出∠DOE的度数.
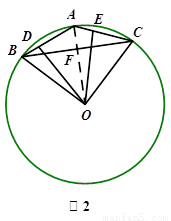
试题解析:解:(1)证明:连接OA、OB、OC,
∵点A是弧BC的中点,∴∠AOB=∠AOC
∵OA=OC =OB, ∴∠ABO=∠BAO=∠OAC=∠ACO
∵AD=CE ∴△AOD≌△COE ∴OD=OE 4分
(2)解:连接BC交OA于点F
∵AB=AC ∴OA⊥BC ∴BF=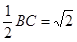
在Rt△BFO中,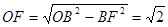 ∴BF=OF∴∠AOB=45°∵△AOD≌△COE∴∠AOD=∠COE
∴BF=OF∴∠AOB=45°∵△AOD≌△COE∴∠AOD=∠COE
∴∠BOD=∠AOE ∴∠DOE=∠AOB=45° 8分
考点:1、垂径定理;2、圆心角、弧、弦之间的关系定理.


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
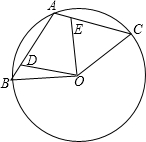 已知A、B、C是半径为2的圆O上的三个点,其中点A是弧BC的中点,连接AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE.
已知A、B、C是半径为2的圆O上的三个点,其中点A是弧BC的中点,连接AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《圆》(12)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com