
分析 根据因式分解法,可得的值,根据勾股定理,可得斜边,根据余弦等于邻边比斜边,可得答案.
解答 解:因式分解,可得Rt△ABC的两条边的值,
(2x-1)(x-1)=0,
解得x=$\frac{1}{2}$,x=1.
2x2-3x+1=0的两个根分别是Rt△ABC的两条边,△ABC最小的角为∠A,得
当BC=$\frac{1}{2}$,AC=1时,
由勾股定理,得
AB=$\sqrt{{(\frac{1}{2})}^{2}{+1}^{2}}$=$\frac{\sqrt{5}}{2}$,
cosA=$\frac{AC}{AB}$=$\frac{1}{\frac{\sqrt{5}}{2}}$=$\frac{2\sqrt{5}}{5}$,
当BC=$\frac{1}{2}$,AB=1时,
由勾股定理,得
AC=$\sqrt{{1}^{2}{-(\frac{1}{2})}^{2}}$=$\frac{\sqrt{3}}{2}$,
∴cosA=$\frac{AC}{AB}$=$\frac{\sqrt{3}}{2}$
综上所述,
故答案为:$\frac{2\sqrt{5}}{5}$或$\frac{\sqrt{3}}{2}$.
点评 此题主要考查了因式分解法解方程以及勾股定理和锐角三角函数关系等知识,利用分类讨论得出是解题关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.7×105 | B. | 0.7×106 | C. | 7×105 | D. | 7×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:单选题
平面内两个正六边形有一边AB重合在一起,将左侧的正六边形绕平面内的某一点,旋转一定的角度后能与右侧的正六边形完全重合,平面内这样的旋转中心有( )个。

A. 1 B. 3 C. 5 D. 无数
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省无锡市八年级3月月考数学试卷(解析版) 题型:填空题
如图,在平面直角坐标系中,点A的坐标为(1,1),OA=AC,∠OAC=90°,点D为x轴上一动点,以AD为边在AD的右侧作正方形ADEF.
(1)如图(1)当点D在线段OC上时(不与点O、C重合),则线段CF与OD之间的数量关系为 ;位置关系为 .
(2)如图(2)当点D在线段OC的延长线上时,(1)中的结论是否成立?若成立,请说明理由;若不成立,请举一反例;
(3)设D点坐标为(t,0),当D点从O点运动到C点时,用含t的代数式表示E点坐标,并直接写出E点所经过的路径长.

查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省无锡市八年级3月月考数学试卷(解析版) 题型:单选题
如图,点D、E、F分别是△ABC三边的中点,则下列判断错误的是( )
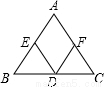
A. 四边形AEDF一定是平行四边形 B. 若∠A=90°,则四边形AEDF是矩形
C. 若AD平分∠A,则四边形AEDF是正方形 D. 若AD⊥BC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省东台市第四教育联盟八年级下学期第一次月考数学试卷(解析版) 题型:填空题
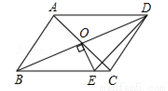
如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则 ABCD的周长为_____cm.
ABCD的周长为_____cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com