
【题目】如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与C重合,D与G重合.若长方形的长BC为8,宽AB为4,求: 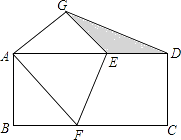
(1)CF的长;
(2)EF的长;
(3)求阴影部分三角形GED的面积.
【答案】
(1)解:设CF=x,则BF=8﹣x,
在Rt△ABF中,AB2+BF2=AF2,
∴16+(8﹣x)2=x2,
解得:x=5,
∴CF=5
(2)解:过F点作FH⊥AD于H,则
FH=4,EH=AE﹣AH=2,
∴EF2=42+22=20,
∴EF=2 ![]()
(3)解:过G点作GM⊥AD于M,则AG×GE=AE×GM,AG=AB=4,AE=CF=5,GE=DE=3,
∴GM= ![]() ,
,
∴S△GED= ![]() ×GM×DE=
×GM×DE= ![]() .
.

【解析】(1)设CF=x,则BF=8﹣x,在Rt△ABF中,AB2+BF2=AF2 , 解方程可求出CF的长;(2)过F点作FH⊥AD于H,在Rt△EHF中根据勾股定理可求出EF的长;(3)过G点作GM⊥AD于M,根据三角形面积不变性,AG×GE=AE×GM,求出GM的长,根据三角形面积公式计算即可.
【考点精析】通过灵活运用翻折变换(折叠问题),掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,直L交AB、CD分别于点E、F,点M在线段EF上(点M不与E、F重合),N是直线CD上的一个动点(点N不与F重合)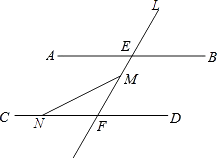
(1)当点N在射线FC上运动时(F点除外),则∠FMN+∠FNM=∠AEF,说明理由?
(2)当点N在射线FD上运动时(F点除外),∠FMN+∠FNM与∠AEF有什么关系?画出图形,猜想结论并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图 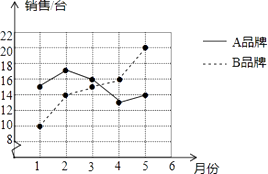
(1)分别求该商场这段时间内A,B两种品牌冰箱月销售量的中位数和方差;
(2)根据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,AC是⊙O的直径,D是![]() 的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E.
的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E. 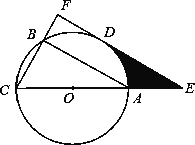
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若CF=6,∠ACB=60°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a、b、c在数轴上的位置如图: ![]()
(1)判断正负,用“>”或“<”填空:b﹣c0,
a+b0,c﹣a0.
(2)化简:|b﹣c|+|a+b|﹣|c﹣a|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式不成立的是( )
A. (m-4)(m+4)=m2-16
B. m(m+4)=m2+4m
C. (m-4)2=m2-8m+16
D. (m+3)2=m2+3m+9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com