
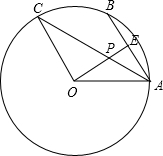
 如图,点A、B、C是⊙O上的三点,AB∥OC.
如图,点A、B、C是⊙O上的三点,AB∥OC.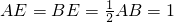 ,
, AE=
AE= ,
,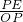 =
=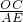 ,即
,即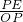 =
= ,
,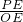 =
= ,
, OE=
OE= ;
;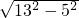 =12,
=12,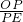 =
=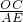 ,
,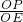 =
=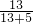 ,
, ×12=
×12= .
. AB=1,再由∠AOE=30°,∠OEA=90°,得到OE=
AB=1,再由∠AOE=30°,∠OEA=90°,得到OE= AE=
AE= ,然后根据AB∥OC,得到
,然后根据AB∥OC,得到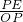 =
=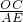 ,即
,即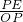 =
= ,利用比例的性质即可得到PE.
,利用比例的性质即可得到PE.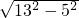 =12,再利用AB∥OC,得到
=12,再利用AB∥OC,得到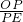 =
=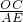 ,利用比例的性质即可得到OP.
,利用比例的性质即可得到OP.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com