
【题目】如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°.
(1)求证:△ABD∽△DCE;
(2)若BD=3,CE=2,求△ABC的边长.

科目:初中数学 来源: 题型:
【题目】已知一次函数y=ax+b(a、b是常数,a≠0)函数图象经过(﹣1,4),(2,﹣2)两点,下面说法中:(1)a=2,b=2;(2)函数图象经过(1,0);(3)不等式ax+b>0的解集是x<1;(4)不等式ax+b<0的解集是x<1;正确的说法有____________________.(请写出所有正确说法的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() (a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<16a;④
(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<16a;④![]() <a<
<a<![]() ;⑤b>c.其中正确结论个数( )
;⑤b>c.其中正确结论个数( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c与直线y=﹣x+6分别交于x轴和y轴上同一点,交点分别是点B和点C,且抛物线的对称轴为直线x=4.
(1)求出抛物线与x轴的两个交点A,B的坐标.
(2)试确定抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=![]() ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=![]() ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=![]() ,其中正确结论为( )
,其中正确结论为( )
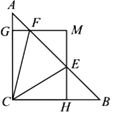
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=![]() .
.
(1)写出此二次函数图象的对称轴;
(2)在如图中建立平面直角坐标系,并画出该函数的图象.(列表、描点、连线)
(3)结合图象回答问题:
①当x的取值范围是 时,y≤0?
②将此抛物线向 平移 个单位时,它与x轴有且只有一个公共点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,猜想:四边形DFBE是什么特殊的四边形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的![]() 的方格中,
的方格中,![]() 和
和![]() 的顶点都在格点上,且
的顶点都在格点上,且![]() .利用平移、旋转变换,能使
.利用平移、旋转变换,能使![]() 通过一次或两次变换后与
通过一次或两次变换后与![]() 完全重合.
完全重合.

(1)请你写出![]() 通过两次变换与
通过两次变换与![]() 完全重合的变换过程.
完全重合的变换过程.
(2)![]() 通过一次旋转就能得到
通过一次旋转就能得到![]() .请在图中标出旋转中心
.请在图中标出旋转中心![]() ,并简要说明你是如何确定的.
,并简要说明你是如何确定的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com