
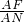 与
与 是否相等?请你说明理由;
是否相等?请你说明理由;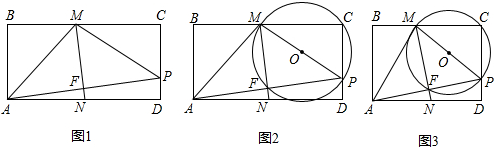
 解:
解: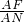 与
与 不相等.
不相等.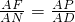 ,
,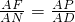 不成立;
不成立;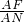 与
与 不相等.
不相等.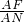

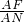 =
=
 ≠
≠
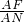 ≠
≠ ;
;
 (4-x)
(4-x) MP=4-OJ=
MP=4-OJ= (4+x)
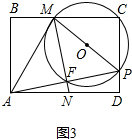
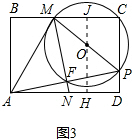
(4+x) MP的长为半径作⊙O,则⊙O过M,P,C三点;
MP的长为半径作⊙O,则⊙O过M,P,C三点;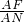 ,在Rt△ADP中,cos∠PAD=
,在Rt△ADP中,cos∠PAD= ,由∠FAN=∠PAD,可得:
,由∠FAN=∠PAD,可得: =
= ,又P与D不重合,故
,又P与D不重合,故 ≠
≠ ,可得:
,可得: 与
与 是不相等;
是不相等; PC,OH=AB-OJ可求出⊙O的半径,又MC=AB,故在Rt△MCP中,运用勾股定理可将PD的长求出.
PC,OH=AB-OJ可求出⊙O的半径,又MC=AB,故在Rt△MCP中,运用勾股定理可将PD的长求出.

科目:初中数学 来源: 题型:
| AF |
| AN |
| AP |
| AD |
查看答案和解析>>
科目:初中数学 来源: 题型:
| AF |
| AN |
| AP |
| AD |
| 1 |
| 2 |
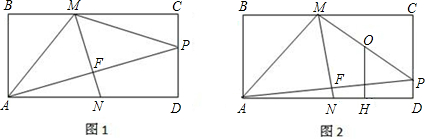 形ABCD的边AB为4,试确定P点的位置(图2供分析参考用)
形ABCD的边AB为4,试确定P点的位置(图2供分析参考用)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
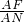 与
与 是否相等?请说明你的理由.
是否相等?请说明你的理由. MP;设矩
MP;设矩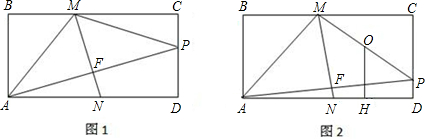 形ABCD的边AB为4,试确定P点的位置(图2供分析参考用)
形ABCD的边AB为4,试确定P点的位置(图2供分析参考用)查看答案和解析>>
科目:初中数学 来源:第3章《圆》中考题集(39):3.2 点、直线与圆的位置关系,圆的切线(解析版) 题型:解答题
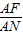 与
与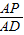 是否相等?请你说明理由;
是否相等?请你说明理由;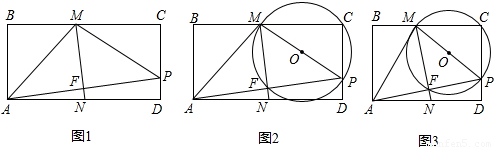
查看答案和解析>>
科目:初中数学 来源:第26章《圆》中考题集(50):26.5 直线与圆的位置关系(解析版) 题型:解答题
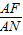 与
与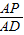 是否相等?请你说明理由;
是否相等?请你说明理由;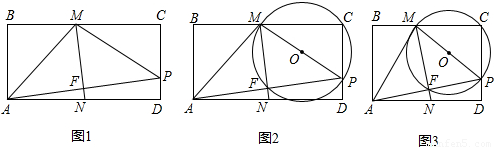
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com