
|
|
| 2 |
| 3 |
| 20 |
| 3 |
|
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 20 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 10 |
| 3 |
| 2 |
| 3 |
| 20 |
| 3 |
| 2 |
| 3 |
| 20 |
| 3 |
| 2 |
| 3 |
| 20 |
| 3 |
| 2 |
| 3 |
| 20 |
| 3 |
| 2 |
| 3 |
| 20 |
| 3 |
| 1 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2012年北师大版初中数学八年级下5.2数据的收集练习卷(解析版) 题型:解答题
2003年5月,一场抗击非典肺炎的 “战争”在全国各地进行着,为了获得每天感染非典患者,疑似病例患者的数据,需要对十二亿多人进行普查吗?你认为采取什么调查方式更适合?请结合实际情况谈谈你的想法。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
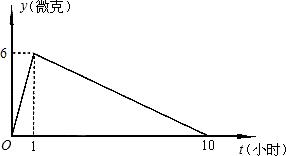
查看答案和解析>>
科目:初中数学 来源:辽宁省期末题 题型:解答题
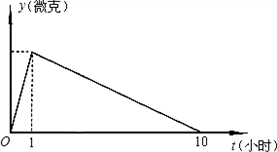
查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《一次函数》(03)(解析版) 题型:解答题
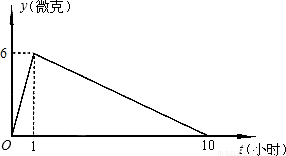
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com