
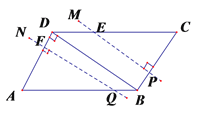
����Ŀ����ͼ������ABCD�У�AD=4cm����A=60����BD��AD.һ����P��A��������ÿ��1cm���ٶ���A��B��C��·�������˶�������P��ֱ��PM��ʹPM��AD.
��1������P�˶�2��ʱ����ֱ��PM��AD�ཻ�ڵ�E������APE�������
��2������P�˶�2��ʱ����һ����QҲ��A������A��B��·���˶�������AB����ÿ��1cm���ٶ������˶�������P��Q�е�ijһ�㵽���յ㣬�����㶼ֹͣ�˶�.����Q��ֱ��QN��ʹQN��PM�����Q�˶���ʱ��Ϊt�루0��t��8����ֱ��PM��QN����ABCD����ͼ�ε����ΪS��cm2��.��S����t�ĺ�����ϵʽ.

���𰸡���1��![]() ����2��
����2��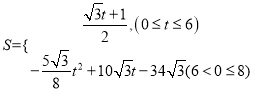 .
.
�����������������(1)����������ó�AP=2AE�������t=2ʱAP��AE��PE�ij��ȣ��Ӷ������APE�������(2)������P��AB��ʱ���Եó�AQ=t��AP=t+2�� ![]() ��
�� ![]() ��
�� ![]() �Ӷ�����ı���PQFE�����������P��BC��ʱ������
�Ӷ�����ı���PQFE�����������P��BC��ʱ������![]() �ó���������ʽ��
�ó���������ʽ��
���������(1)����A=60����PE��AD ��AP=2AE��
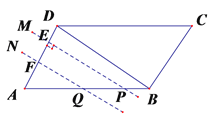
t=2ʱ��AP=2��AE=1��PE=![]() �� ��
�� ��![]() ��
��
(2)����![]() ʱ��P��AB��
ʱ��P��AB��
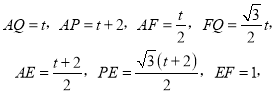
![]()
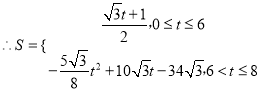 ��
��
���������������Ҫ������Ƕ��������뺯��ͼ�����⣬�Ѷ����ϣ��ڽ���йض��������ʱ������һ��Ҫע����з������ۣ���ÿһ��ȡֵ��Χ֮�ڣ�����Ҫ�����е��߶��ú�δ֪���Ĵ���ʽ�����б�ʾ��Ȼ���������ļ��㷨���������������ʽ�������ڷ������۵�ʱ����Զ������ͼ�Σ�Ȼ��ֱ���м��㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A.5x2��4x3��1B.x2y��xy2��0
C.��3ab��2ab����5abD.2m2+3m3��5m5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��һ�����ù������ݳ���ij�������Σ�С��������ǰ��������35L����ʻ����Сʱ��;���ڼ���վ������������������������Q��L������ʻʱ��t��h��֮��Ĺ�ϵ��ͼ��ʾ������ͼ��ش��������⣺
��1��С������ʻ______h����ͣ���;����_______L
��2�������ǰ����������Q����ʻʱ��t�ĺ�����ϵʽ
��3�����С��������ʻ�����к������ٶȲ��䣬����վ�ྰ��200km������80km/h��Ҫ����Ŀ�ĵأ������е����Ƿ��ã���˵������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ,����ABC����ijһ����ƽ��һ���ľ���õ���MNL,�����н�������ȷ�������� ��
��AM��BN����AM=BN����BC=ML���ܡ�ACB=��MNL��

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ʽx2��16x+m2��һ����ȫƽ��ʽ����ôm��ֵ�ǣ� ��
A.��8B.4C.��4D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У����ǰ��ֱ�Ƕ���P������Ϊ(2��2)��һ��ֱ�DZ���x��������ύ�ڵ�A����һֱ�DZ���y�ύ�ڵ�B�����ǰ��Ƶ�P������ƽ����ת���Ĺ����У�����POAΪ����������ʱ����д���������������ĵ�B������__________��
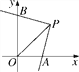
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������һ�������о���120Ԫ���������·�,һ��20��,һ����20��,����ν�����,�����ˣ� ��
A.10ԪB.��10ԪC.������D.��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����AOB=90�㣬��C������OA�ϣ�CD��OE��
��1����ͼ1������OCD=120�㣬���BOE�Ķ�����
��2���ѡ���AOB=90�㡱��Ϊ����AOB=120�㡱������OE������OBƽ�ƣ���O��E�������������䣬����ͼ2��ʾ����̽����OCD����BO��E��������ϵ��
��3���ڣ�2���������£���PO���OB����ΪO�䣬���OCD��ƽ����CP���ڵ�P������BO��E=�������ú�����ʽ�ӱ�ʾ��CPO�䣨��ֱ��д���𰸣���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com