
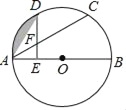
【题目】如图,点C,D是半圆O上的三等分点,直径AB=4,连接AD,AC,作DE⊥AB,垂足为E,DE交AC于点F.
(1)求证:AF=DF.
(2)求阴影部分的面积(结果保留π和根号)
【答案】(1)证明见解析;(2)![]() ;
;
【解析】
(1)连接OD,OC,根据已知条件得到∠AOD=∠DOC=∠COB=60°,根据圆周角定理得到∠CAD=∠ADE=30°,于是得到结论;
(2)由(1)知,∠AOD=60°,推出△AOD是等边三角形,OA=2,得到DE=![]() ,根据扇形和三角形的面积公式即可得到结论
,根据扇形和三角形的面积公式即可得到结论
(1)证明:连接OD,OC,
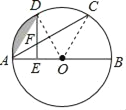
∵C、D是半圆O上的三等分点,
∴![]() =
=![]() =
=![]() ,度数都是60°,
,度数都是60°,
∴∠AOD=∠DOC=∠COB=60°,
∴∠DAC=30°,∠CAB=30°,
∵DE⊥AB,
∴∠AEF=90°,
∴∠ADE=180°﹣90°﹣30°﹣30°=30°,
∴∠DAC∠ADE=30°,
∴AF=DF;
(2)解:由(1)知,∠AOD=60°,
∵OA=OD,AB=4,
∴△AOD是等边三角形,OA=2,
∵DE⊥AO,
∴DE=![]() ,
,
∴S阴影=S扇形AOD﹣S△AOD=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知⊙O的直径为10,点A、点B、点C在⊙O上,∠CAB的平分线交⊙O于点D.


(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD的长;
(2)如图②,若∠CAB=60°,CF⊥BD,①求证:CF是⊙O的切线;②求由弦CD、CB以及弧DB围成图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AD是△ABC的中线,AE∥BC,射线BE交AD于点F,交⊙O于点G,点F是BE的中点,连接CE.
(1)求证:四边形ADCE为平行四边形;
(2)若BC=2AB,求证: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com