
分析 (1)根据方程无解,即(x-2)(x+1)=0,解得:x=2或x=-1,再代入整式方程即可解答;
(2)根据方程有解,即(x-2)(x+1)≠0,解得:x≠2或x≠-1,再代入整式方程即可解答;
(3)根据方程的解为正数,列出不等式,即可解答.
解答 解:在方程两边同乘以(x-2)(x+1)得:(x-1)(x+1)-(x-2)(x-2)=2x+a,
整理得:a=2x-5,
(1)当方程无解,即(x-2)(x+1)=0,
解得:x=2或x=-1,
当x=2时,a=-1,
当x=-1时,a=-7,
∴当a为-1或-7时,方程无解;
(2)当方程有解,即(x-2)(x+1)≠0,
解得:x≠2或x≠-1,
当x≠2时,a≠-1,
当x≠-1时,a≠-7,
∴当a≠-1或a≠-7时,方程有解;
(3)a=2x-5,
x=$\frac{a+5}{2}$,
∵方程的解为正数,
∴$\frac{a+5}{2}>0$,
解得:a>-5.
点评 本题考查了分式方程的解,解决本题的关键是明确分式方程无解、有解的条件.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
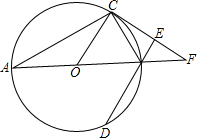 如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,过C作⊙O的切线交AB的延长线于点F,DB⊥CF,垂足为E.
如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,过C作⊙O的切线交AB的延长线于点F,DB⊥CF,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
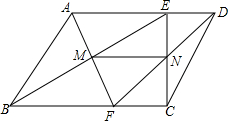 如图,在平行四边形ABCD中,E,F分别是AD,BC上的点,且AE=BF,BE交AF于M,CE交DF于N,求证:MN$\stackrel{∥}{=}$$\frac{1}{2}$AD.
如图,在平行四边形ABCD中,E,F分别是AD,BC上的点,且AE=BF,BE交AF于M,CE交DF于N,求证:MN$\stackrel{∥}{=}$$\frac{1}{2}$AD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在行驶过程中的平均速度为$\frac{80}{3}$千米/小时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.其中正确的说法共有( )
一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在行驶过程中的平均速度为$\frac{80}{3}$千米/小时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.其中正确的说法共有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com