
问题情境:将一副直角三角板(Rt△ABC和Rt△DEF)按图1所示的方式摆放,其中∠ACB=90°,CA=CB,∠FDE=90°,O是AB的中点,点D与点O重合,DF⊥AC于点M,DE⊥BC于点N,试判断线段OM与ON的数量关系,并说明理由.
探究展示:小宇同学展示出如下正确的解法:
解:OM=ON,证明如下:
连接CO,则CO是AB边上中线,
∵CA=CB,∴CO是∠ACB的角平分线.(依据1)
∵OM⊥AC,ON⊥BC,∴OM=ON.(依据2)
反思交流:
(1)上述证明过程中的“依据1”和“依据2”分别是指:
依据1: ;
依据2: .
(2)你有与小宇不同的思考方法吗?请写出你的证明过程.
拓展延伸:
(3)将图1中的Rt△DEF沿着射线BA的方向平移至如图2所示的位置,使点D落在BA的延长线上,FD的延长线与CA的延长线垂直相交于点M,BC的延长线与DE垂直相交于点N,连接OM、ON,试判断线段OM、ON的数量关系与位置关系,并写出证明过程.
(1)依据1为:等腰三角形三线合一(或等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合),依据2为:角平分线上的点到角的两边距离相等;
(2)见解析;
(3)OM=ON,OM⊥ON.理由见解析.
解析试题分析:(1)根据等腰三角形的性质和角平分线性质得出即可;
(2)证△OMA≌△ONB(AAS),即可得出答案;
(3)求出矩形DMCN,得出DM=CN,△MOC≌△NOB(SAS),推出OM=ON,∠MOC=∠NOB,得出∠MOC-∠CON=∠NOB-∠CON,求出∠MON=∠BOC=90°,即可得出答案.
(1)解:依据1为:等腰三角形三线合一(或等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合),依据2为:角平分线上的点到角的两边距离相等.
(2)证明:∵CA=CB,
∴∠A=∠B,
∵O是AB的中点,
∴OA=OB.
∵DF⊥AC,DE⊥BC,
∴∠AMO=∠BNO=90°,
∵在△OMA和△ONB中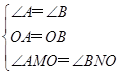 ,
,
∴△OMA≌△ONB(AAS),
∴OM=ON.
(3)解:OM=ON,OM⊥ON.理由如下:
如图2,连接OC,
∵∠ACB=∠DNB,∠B=∠B,
∴△BCA∽△BND,
∴ ,
,
∵AC=BC,
∴DN=NB.
∵∠ACB=90°,
∴∠NCM=90°=∠DNC,
∴MC∥DN,
又∵DF⊥AC,
∴∠DMC=90°,
即∠DMC=∠MCN=∠DNC=90°,
∴四边形DMCN是矩形,
∴DN=MC,
∵∠B=45°,∠DNB=90°,
∴∠3=∠B=45°,
∴DN=NB,
∴MC=NB,
∵∠ACB=90°,O为AB中点,AC=BC,
∴∠1=∠2=45°=∠B,OC=OB(斜边中线等于斜边一半),
在△MOC和△NOB中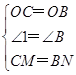 ,
,
∴△MOC≌△NOB(SAS),
∴OM=ON,∠MOC=∠NOB,
∴∠MOC-∠CON=∠NOB-∠CON,
即∠MON=∠BOC=90°,
∴OM⊥ON.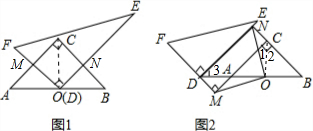
考点:全等三角形的判定与性质;角平分线的性质;等腰三角形的性质;矩形的判定与性质.


科目:初中数学 来源: 题型:解答题
如图,直线AC∥DF,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角板,于是他想了这样一个办法:首先连结CF,再找出CF的中点O,然后连结EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF。
以下是他的想法,请你填上根据。小华是这样想的:
因为CF和BE相交于点O,
根据 得出∠COB=∠EOF;
而O是CF的中点,那么CO=FO,又已知 EO=BO,
根据 得出△COB≌△FOE,
根据 得出BC=EF,
根据 得出∠BCO=∠F,
既然∠BCO=∠F,根据 出AB∥DF,
既然AB∥DF,根据 得出∠ACE和∠DEC互补.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.请将解题过程填写完整.
解:∵EF∥AD(已知)
∴∠2= _________ ( )
又∵∠1=∠2(已知)
∴∠1=∠3( )
∴AB∥ _________ ( )
∴∠BAC+ _________ =180°( )
∵∠BAC=70°(已知)
∴∠AGD= _________ .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图①所示,已知,BC∥OA,∠B=∠A=100°,试回答下列问题:
⑴试说明:OB∥AC;
⑵如图②,若点E、F在BC上,且∠FOC=∠AOC ,OE平分∠BOF.试求∠EOC的度数;
⑶在⑵的条件下,若左右平行移动AC,如图③,那么∠OCB:∠OFB的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;
⑷在⑶的条件下,当∠OEB=∠OCA时,试求∠OCA的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com