
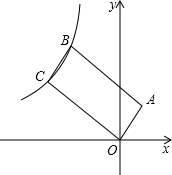
 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过平行四边形OABC的两个顶点B,C,若点A的坐标为(1,2),AB=$\sqrt{5}$BC,则反比例函数的解析式为y=-$\frac{12}{x}$或y=-$\frac{119}{25x}$.
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过平行四边形OABC的两个顶点B,C,若点A的坐标为(1,2),AB=$\sqrt{5}$BC,则反比例函数的解析式为y=-$\frac{12}{x}$或y=-$\frac{119}{25x}$. 分析 由点A坐标可得OA长,根据平行四边形性质可得OC的长,设点C坐标为(x,$\frac{k}{x}$),则点B坐标为(x+1,$\frac{k}{x}$+2),由勾股定理可得x2+$\frac{{k}^{2}}{{x}^{2}}$=25,由点B在双曲线上可得$\frac{k}{x}$+2=$\frac{k}{x+1}$,解方程组可得k的值.
解答 解:∵点A的坐标为(1,2),
∴OA=$\sqrt{5}$,
又∵四边形OABC是平行四边形,且AB=$\sqrt{5}$BC,
∴OC=5,
∵点C在双曲线y=$\frac{k}{x}$上,
∴设点C坐标为(x,$\frac{k}{x}$),
则x2+$\frac{{k}^{2}}{{x}^{2}}$=25 ①,
根据题意知点B的坐标为(x+1,$\frac{k}{x}$+2),
又∵点B在双曲线y=$\frac{k}{x}$上,
∴$\frac{k}{x}$+2=$\frac{k}{x+1}$ ②,
由②可得,k=-2x2-2x,代入①整理得:5x2+8x-21=0,
解得:x=-3或x=$\frac{7}{5}$,
当x=-3时,k=-2x2-2x=-12,
当x=$\frac{7}{5}$时,k=-2x2-2x=-$\frac{119}{25}$,
∴反比例函数的解析式为:y=-$\frac{12}{x}$或y=-$\frac{119}{25x}$.
故答案为:y=-$\frac{12}{x}$或y=-$\frac{119}{25x}$.
点评 本题主要考查反比例函数解析式求法及平行四边形的性质,设出C两点坐标,根据平行四边形性质表示出点B坐标是前提,运用勾股定理和反比例函数图象上点的坐标特点列出方程是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知抛物线m经过原点O,与x轴交于点A(-3,0),P为抛物线的顶点将抛物线m平移后得到抛物线y=(x+$\frac{3}{2}$)2,其中点A,P,O的对应点分别为A′,P′,O′,连接AA′,则图中阴影部分的面积为$\frac{27}{4}$.
如图,已知抛物线m经过原点O,与x轴交于点A(-3,0),P为抛物线的顶点将抛物线m平移后得到抛物线y=(x+$\frac{3}{2}$)2,其中点A,P,O的对应点分别为A′,P′,O′,连接AA′,则图中阴影部分的面积为$\frac{27}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论成立的是①②③(将正确番号填入)
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论成立的是①②③(将正确番号填入)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
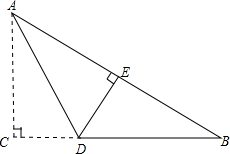 如图,Rt△ABC中,∠C=90°,现将直角边AC折叠到AB边上,点C落在AB边上的E点,折痕为AD,若AC=6,BC=8.求△ADB的面积.
如图,Rt△ABC中,∠C=90°,现将直角边AC折叠到AB边上,点C落在AB边上的E点,折痕为AD,若AC=6,BC=8.求△ADB的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
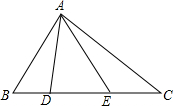 在△ABC中,AB=14,AE=12,BD=7,BC=28,且∠BAD=∠EAC.
在△ABC中,AB=14,AE=12,BD=7,BC=28,且∠BAD=∠EAC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
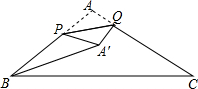 如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )
如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )| A. | 2$\sqrt{3}$-2 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
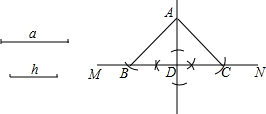
| A. | (1) | B. | (2) | C. | (3) | D. | (4) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是520 cm.
如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是520 cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com