
已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连结DE.
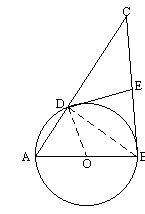
(1)如图,求证:DE是⊙O的切线;
(2)连结OE、AE,当∠CAB为何值时,四边形AOED是平行四边形,并在此条件下求sin∠CAE的值.
(第(2)问答题要求:不要求写出解题过程,只需将结果填写在答题卡相应题号的横线上.)
|
(1)证法一: 连结DO,OB ∵AB是⊙O的直径 ∴∠ADB= ∴∠CDB= ∵E为BC边上的中点 ∴CE=EB=DE ∴∠1=∠2 ∵OB=OD ∴∠3=∠4 ∴∠1+∠4=∠2+∠3 ∵在Rt△ABC中,∠ABC=∠2+∠3= ∴∠EDO=∠1+∠4= ∵D为⊙O上的点 ∴DE是⊙O的切线 证法二:连结OD,OE
∵OA=OD ∴∠1=∠2 ∵E为BC边上的中点,O为AB边上的中点 ∴OE∥AC ∴∠1=∠3,∠2=∠4 ∴∠3=∠4 ∵OD=OB,OE=OE ∴△EDO≌△EBO ∴∠EDO=∠EBO ∴△ABC为直角三角形 ∴∠EBO= ∴∠EDO= ∵D为⊙O上的点 ∴DE是⊙O的切线 (2)解:∠CAB= sin∠CAE= |
|
根据切线的性质定理:圆的切线垂直于经过切点的半径,要证明DE是⊙O的切线,只需证明∠EDO=
|


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
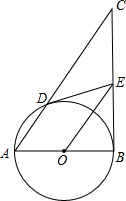 已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,过点D作⊙O的切线交BC边于点E.
已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,过点D作⊙O的切线交BC边于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
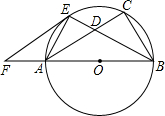 ⊙O于E,过E作EF∥AC交BA的延长线于F.AF=5,EF=10,
⊙O于E,过E作EF∥AC交BA的延长线于F.AF=5,EF=10,查看答案和解析>>
科目:初中数学 来源: 题型:
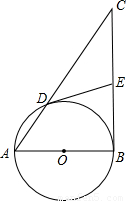
 已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连接DE.
已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连接DE.查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《圆》(12)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2009年广东省深圳市初中毕业模拟试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com