

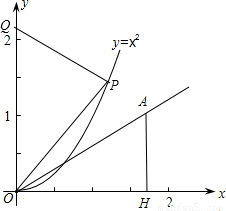
 x,联立抛物线的解析式可得P点坐标,进而可求出OQ、PQ的长,由于△POQ≌△AOH,那么OH=OQ、AH=PQ,由此得到点A的坐标.
x,联立抛物线的解析式可得P点坐标,进而可求出OQ、PQ的长,由于△POQ≌△AOH,那么OH=OQ、AH=PQ,由此得到点A的坐标. 解:①当∠POQ=∠OAH=60°,若以P,O,Q为顶点的三角形与△AOH全等,那么A、P重合;
解:①当∠POQ=∠OAH=60°,若以P,O,Q为顶点的三角形与△AOH全等,那么A、P重合; x,联立抛物线的解析式,
x,联立抛物线的解析式, ,
, ,
, ;
; ,
, );
);
 x,联立抛物线的解析式,
x,联立抛物线的解析式, ,
, ,
, ;
; ,3),那么A(3,
,3),那么A(3, );
);
 x,联立抛物线的解析式,
x,联立抛物线的解析式, ,
, 、
、 ,
, ,3),
,3), ,QP=2,
,QP=2, ,AH=QP=2,
,AH=QP=2, ,2);
,2);
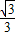 x,联立抛物线的解析式,
x,联立抛物线的解析式, ,
, 、
、 ,
, ,
, ),
), ,OP=
,OP= ,
, ,AH=OP=
,AH=OP= ,
, ,
, ).
). ,
, )或(3,
)或(3, )或(2
)或(2 ,2)或(
,2)或( ,
, ).
).

科目:初中数学 来源:2010年北京市宣武区中考数学一模试卷(解析版) 题型:解答题
 的图象向上平移2个单位,得到一个新的函数图象.
的图象向上平移2个单位,得到一个新的函数图象. 交于C,B两点.试判断以A,B,C,O四点为顶点四边形形状,并说明理由;
交于C,B两点.试判断以A,B,C,O四点为顶点四边形形状,并说明理由; 的图象一部分,求满足条件的实数b的取值范围.
的图象一部分,求满足条件的实数b的取值范围.
查看答案和解析>>
科目:初中数学 来源:2010年北京市宣武区中考数学一模试卷(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2010年江苏省扬州市扬州中学西区校中考数学三模试卷(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2010年北京市宣武区中考数学一模试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com