
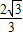 kx+m(-
kx+m(- ≤k≤
≤k≤ )经过点A(
)经过点A( ,4),且与y轴相交于点C.点B在y轴上,O为坐标原点,且OB=OA+7-2
,4),且与y轴相交于点C.点B在y轴上,O为坐标原点,且OB=OA+7-2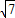 .记△ABC的面积为S.
.记△ABC的面积为S.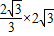 k+m=4,k=1-
k+m=4,k=1- m.因为
m.因为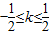 ,即
,即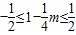 .解得2≤m≤6.
.解得2≤m≤6.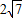 ,OB=7.所以B点的坐标为(0,7)或(0,-7).
,OB=7.所以B点的坐标为(0,7)或(0,-7).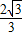 kx+m与y轴的交点为C(0,m).
kx+m与y轴的交点为C(0,m). •2
•2 •BC=
•BC=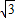 (7-m);
(7-m); •2
•2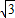 •BC=
•BC=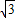 (7+m).
(7+m). ,得∠ACD=60°,∠ACB′=∠ACD=60°,CB′=BC=7-2=5,所以∠B′CE=180°-∠B′CB=60°.
,得∠ACD=60°,∠ACB′=∠ACD=60°,CB′=BC=7-2=5,所以∠B′CE=180°-∠B′CB=60°. ,B′E=
,B′E=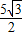 .故OE=CE-OC=
.故OE=CE-OC= .所以点B′的坐标为(
.所以点B′的坐标为(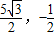 ).
).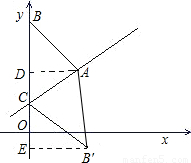 解:(1)∵直线y=
解:(1)∵直线y=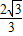 kx+m(-
kx+m(- ≤k≤
≤k≤ )经过点A(
)经过点A(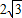 ,4),
,4),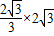 k+m=4,
k+m=4, m.
m. ,∴
,∴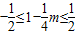 .
.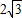 ,4),∴OA=
,4),∴OA=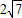 .
.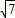 ,∴OB=7.∴B点的坐标为(0,7)或(0,-7).
,∴OB=7.∴B点的坐标为(0,7)或(0,-7).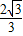 kx+m与y轴的交点为C(0,m).
kx+m与y轴的交点为C(0,m). •2
•2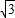 •BC=
•BC=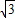 (7-m).
(7-m). •2
•2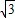 •BC=
•BC=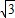 (7+m).
(7+m).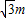 +7
+7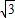 取得最大值
取得最大值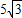 ,这时C(0,2).
,这时C(0,2).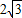 ,CD=4-2=2.
,CD=4-2=2. ,
, ,B′E=
,B′E=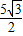 .
. .
.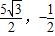 ).
).

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2005年全国中考数学试题汇编《图形的相似》(02)(解析版) 题型:选择题
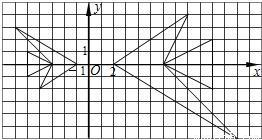
查看答案和解析>>
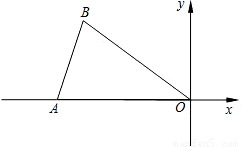
科目:初中数学 来源:2005年全国中考数学试题汇编《图形的平移》(01)(解析版) 题型:解答题
查看答案和解析>>
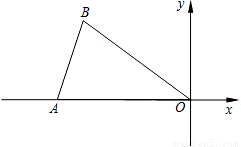
科目:初中数学 来源:2005年全国中考数学试题汇编《图形的对称》(04)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2005年江苏省南通市中考数学试卷(大纲卷)(解析版) 题型:解答题
 kx+m(-
kx+m(- ≤k≤
≤k≤ )经过点A(
)经过点A( ,4),且与y轴相交于点C.点B在y轴上,O为坐标原点,且OB=OA+7-2
,4),且与y轴相交于点C.点B在y轴上,O为坐标原点,且OB=OA+7-2 .记△ABC的面积为S.
.记△ABC的面积为S.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com