
 等.
等. (k是常数,k≠0)的图象在第一,三象限,则k>0,符合上述条件的k的一个值可以是2.(正数即可,答案不唯一);
(k是常数,k≠0)的图象在第一,三象限,则k>0,符合上述条件的k的一个值可以是2.(正数即可,答案不唯一);

 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
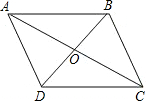 已知四边形ABCD,对角线AC、BD交于点O.现给出四个条件:
已知四边形ABCD,对角线AC、BD交于点O.现给出四个条件:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
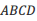 中,有下列三个论断:①
中,有下列三个论断:①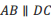 ;②
;②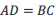 ;③
;③ ;请以其中两个论断作为题设,另一个论断作为结论,写出一个你认为正确的命题.李梅同学写出了命题1:已知四边形
;请以其中两个论断作为题设,另一个论断作为结论,写出一个你认为正确的命题.李梅同学写出了命题1:已知四边形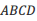 中,
中,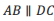 ,
, ,则
,则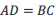 .王华同学写出了命题2:已知四边形
.王华同学写出了命题2:已知四边形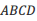 中,
中,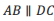 ,
,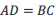 ,则
,则 .你认为命题1和命题2都正确吗?若正确,请加以证明;若不正确,请举反例说明理由.
.你认为命题1和命题2都正确吗?若正确,请加以证明;若不正确,请举反例说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com