解:(1)移项得,5m-4m=6,
合并同类项得,m=6;
∵方程5m-6=4m的解也是关于x的方程2(x-3)-n=4的解,
∴2(6-3)-n=4,
解得n=2;
(2)①如图1,点P在线段AB上时,
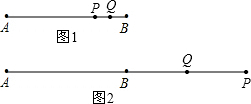
∵AB=6,

=2,
∴AP=6×
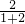
=4,
PB=AB-AP=6-4=2,
∵点Q为PB的中点,
∴PQ=

PB=1,
∴AQ=AP+PQ=4+1=5;
②如图2,点P在线段AB的延长线上时,
∵AB=6,

=2,
∴

=2,
解得BP=6,
∵点Q为PB的中点,
∴BQ=

BP=3,
∴AQ=AB+BQ=6+3=9,
综上,线段AQ的长为5或9.
故答案为:(1)6,2,(2)5或9.
分析:(1)先求出第一个方程的解,然后根据方程同解把第二个方程中的x换成m的值,求解即可得到n的值;
(2)分①点P在线段AB上时,先根据比值求出AP,PB的长度,再根据中点定义求出PQ的长度,相加即可求出AQ的长度;
②点P在线段AB的延长线上时,根据比值求出BP的长度,再根据中点定义求出BQ的长度,相加即可求出AQ的长度.
点评:本题考查了同解方程以及线段的中点的定义,先求出一个可以容易求解的方程的解是求解同解方程问题的关键,本题需要注意,第一个方程的m的值是第二个方程中的x的值.

 已知方程5m-6=4m的解也是关于x的方程2(x-3)-n=4的解.
已知方程5m-6=4m的解也是关于x的方程2(x-3)-n=4的解.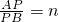 ,点Q为PB的中点,求线段AQ的长.
,点Q为PB的中点,求线段AQ的长.
 =2,
=2,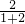 =4,
=4, PB=1,
PB=1, =2,
=2, =2,
=2, BP=3,
BP=3,

 习题精选系列答案
习题精选系列答案 已知方程5m-6=4m的解也是关于x的方程2(x-3)-n=4的解.
已知方程5m-6=4m的解也是关于x的方程2(x-3)-n=4的解.