
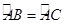 ,在此圆形铁皮中剪下一个扇形(阴影部分).
,在此圆形铁皮中剪下一个扇形(阴影部分). );
);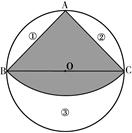
 ∵
∵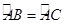 ∴AB=AC,
∴AB=AC, 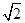
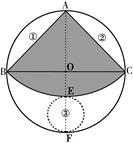
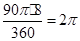 ;
; 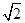 R
R 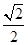 πR
πR 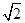 R,以EF为直径作圆,是剩余材料中所作的最大的圆,其圆周长为:(2-
R,以EF为直径作圆,是剩余材料中所作的最大的圆,其圆周长为:(2-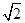 )πR
)πR 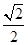 πR>(2-
πR>(2-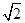 )πR
)πR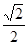 Rπ,以EF为直径作圆,是剩余材料中所作的最大的圆,求出其周长为(2-
Rπ,以EF为直径作圆,是剩余材料中所作的最大的圆,求出其周长为(2-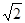 )Rπ,比较大小可知不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.
)Rπ,比较大小可知不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.

科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止.请你根据题意,在图上画出圆心O运动路径的示意图;圆心O运动的路程是 ▲ .
,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止.请你根据题意,在图上画出圆心O运动路径的示意图;圆心O运动的路程是 ▲ .
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
A.36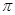 | B.54 | C.27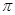 | D.128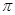 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
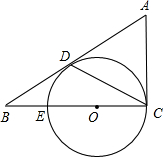
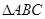 内接于⊙
内接于⊙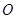 ,
,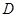 为线段
为线段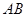 的中点,延长
的中点,延长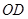 交⊙
交⊙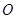 于点
于点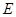 ,连结
,连结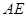 ,
,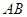 ,则下列五个结论:①
,则下列五个结论:①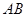 ⊥
⊥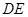 ,②
,②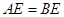 ,③
,③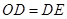 ,④
,④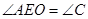 ,⑤
,⑤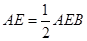 ,正确结论的个数有( )
,正确结论的个数有( )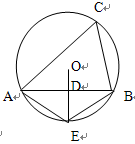
A. 个 个 | B.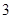 个 个 | C.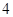 个 个 | D.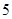 个 个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com