
【题目】解答
(1)求不等式 ![]() ﹣
﹣ ![]() ≤
≤ ![]() 的非负整数解;
的非负整数解;
(2)若关于x的方程2x﹣3m=2m﹣4x+4的解不小于 ![]() ﹣
﹣ ![]() ,求m的最小值.
,求m的最小值.
【答案】
(1)解:原不等式可化为: ![]() ﹣﹣
﹣﹣ ![]() ≤
≤ ![]() ,
,
去分母,得6(4x﹣10)﹣15(5﹣x)≤10(3﹣2x),
去括号,得24x﹣60﹣75+15x≤30﹣20x,
移项,得24x+15x+20x≤30+60+75,
合并同类项,得59x≤165,
把系数化为1,得x≤ ![]() ,
,
所以原不等式的非负整数解是:0,1,2
(2)解:关于x的方程2x﹣3m=2m﹣4x+4的解为:x= ![]() .
.
根据题意,得 ![]() ≥
≥ ![]() ﹣
﹣ ![]() ,
,
去分母,得4(5m+4)≥21﹣8(1﹣m),
去括号,得20m+16≥21﹣8+8m,
移项,合并同类项得12m≥﹣3,
系数化为1,得m≥﹣ ![]() .
.
所以当m≥﹣ ![]() 时,方程的解不小于
时,方程的解不小于 ![]() ﹣
﹣ ![]() ,
,
所以m的最小值为﹣ ![]()
【解析】(1)首先利用分数的基本性质,将分子、分母上的小数化成整数,然后根据不等式的性质2去掉分母等进行求解不等式,再在解集中求出符合条件的非负整数;(2)首先求解关于x的方程2x﹣3m=2m﹣4x+4,即可求得x的值,根据方程的解的解不小于 ![]() ﹣
﹣ ![]() ,即可得到关于m的不等式,即可求得m的范围,从而求解.
,即可得到关于m的不等式,即可求得m的范围,从而求解.
【考点精析】解答此题的关键在于理解一元一次不等式的整数解的相关知识,掌握大大取较大,小小取较小;小大,大小取中间;大小,小大无处找.


科目:初中数学 来源: 题型:
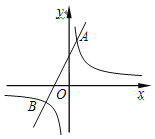
【题目】已知一次函数y1=2x+m的图象与反比例函数y2=![]() 的图象交于A,B两点,且点A的横坐标为1.
的图象交于A,B两点,且点A的横坐标为1.
(1)求一次函数的表达式;
(2)若反比例函数在第一象限的图象上有一点C到y轴的距离为3,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
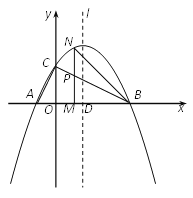
【题目】如图,已知抛物线![]() (其中
(其中![]() )与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
(1)求抛物线的关系式;
(2)过点![]() 的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了奖励在数学竞赛中获奖的学生,买了若干本课外读物准备送给他们,如果每人送3本,则还余8本;如果前面每人送5本,则最后一人得到的课外读物不足3本,设该校买了m本课外读物,有x名学生获奖,请解答下列问题:
(1)用含x的代数式表示m;
(2)求出该校的获奖人数及所买课外读物的本数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,D(0,﹣3),M(4,﹣3),直角三角形ABC的边与x轴分别交于O、G两点,与直线DM分别交于E、F点. 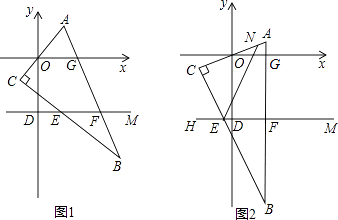
(1)将直角三角形ABC如图1位置摆放,请写出∠CEF与∠AOG之间的等量关系: .
(2)将直角三角形ABC如图2位置摆放,N为AC上一点,∠NED+∠CEF=180°,请写出∠NEF与∠AOG之间的等量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com