练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，已知点E、F在四边形ABCD的对角线延长线上，AE=CF，DE∥BF，∠1=∠2．

    （1）求证：△AED≌△CFB；

    （2）若AD⊥CD，四边形ABCD是什么特殊四边形？请说明理由．


    （1）证明：∵DE∥BF，

    ∴∠E=∠F，

    在△AED和△CFB中，

    ，

    ∴△AED≌△CFB（AAS）；

    （2）解：四边形ABCD是矩形．

    理由如下：∵△AED≌△CFB，

    ∴AD=BC，∠DAE=∠BCF，

    ∴∠DAC=∠BCA，

    ∴AD∥BC，

    ∴四边形ABCD是平行四边形，

    又∵AD⊥CD，

    ∴四边形ABCD是矩形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    不等式3x+2＞﹣1的解集是（　　）

    　  A．             x＞﹣             B． x＜﹣          C． x＞﹣1   D． x＜﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，海中有一灯塔P，它的周围8海里内有暗礁．海轮以18海里/时的速度由西向东航行，在A处测得灯塔P在北偏东60°方向上；航行40分钟到达B处，测得灯塔P在北偏东30°方向上；如果海轮不改变航线继续向东航行，有没有触礁的危险？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    从一栋二层楼的楼顶点A处看对面的教学楼，探测器显示，看到教学楼底部点C处的俯角为45°，看到楼顶部点D处的仰角为60°，已知两栋楼之间的水平距离为6米，则教学楼的高CD是（　　）

    　

    A．

    （6+6）米

    B．

    （6+3）米

    C．

    （6+2）米

    D．

    12米

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，AC=BC，∠B=70°，分别以点A、C为圆心，大于AC的长为半径作弧，两弧相交于点M、N，作直线MN，分别交AC、BC于点D、E，连结AE，则∠AED的度数是　　°．

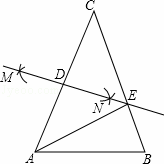
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    等于（   ）

    A．2    B．－2    C．    D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    多项式的项数及次数分别是（   ）

    A．3，3    B．3，2    C．2，3    D．2，2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    我们把“按照某种理想化的要求（或实际可应用的标准）来反映或概括地表现一类或某种事物关系结构的数学形式”看作是数学中的一个“模式”（我国著名数学家徐利浩）

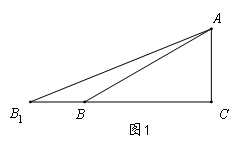
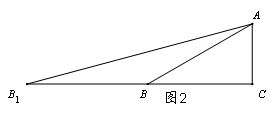
    如图是一个典型的图形模式，用它可以测底部可能达不到的建筑物的高度，用它可测宽，用它可解决数学中的一些问题，等等。

    ⑴如图1，若B1B=30米，∠B1=22°，∠ABC=30°，求AC（精确到1）；

    参考数据：sin22°≈0.37，cos22°≈0.92，tan22°≈0.40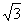，≈1.73

    ⑵如图2，若∠ABC=30°，B1B=AB，计算tan15°的值（保留准确值）；

    ⑶直接写出 tan7.5°的值

    注：若出现双重根式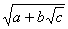，则无需化简；

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，OB是⊙O的半径，弦AB=OB，直径CD⊥AB，若点P是线段OD上的动点，连接PA，则∠PAB的度数可以是             （写出一个即可）.

    查看答案和解析>>

    同步练习册答案