
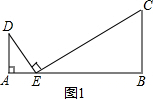
 ��1�����ԣ���ͼ����֪A��E��B������ͬһֱ���ϣ��ҡ�A=��B=��DEC=90�㣬
��1�����ԣ���ͼ����֪A��E��B������ͬһֱ���ϣ��ҡ�A=��B=��DEC=90�㣬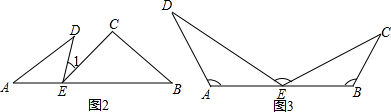
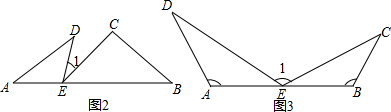
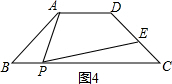 �غϣ�������AP������P��PE��CD�ڵ�E��ʹ�á�APE=��ABC����BPΪ��ֵʱ����EΪCD���е㣮
�غϣ�������AP������P��PE��CD�ڵ�E��ʹ�á�APE=��ABC����BPΪ��ֵʱ����EΪCD���е㣮 | AE |
| BC |
| AD |
| BE |

| AE |
| BC |
| AD |
| BE |
| AE |
| BC |
| AD |
| BE |

| AB |
| PC |
| BP |
| CE |
| 4 |
| 9-x |
| x |
| 2 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���绪��ͬ��ѵ������ѧ�����꼶�²ᣨ�¿α��˽̰棩 �¿α��˽̰� ���ͣ�044
��ͼ����֪AB��CD���ֱ����������ĸ�ͼ���С�A����C����P�Ĺ�ϵ��������˵��������ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�044
��ͼ��Ҫ������������Ե�����A��B��ľ��룬������AB�Ĵ���BF��ȡ����C��D��ʹCD=BC���ٶ���BF�Ĵ���DE��ʹA��C��E��һ��ֱ���ϣ���ʱ��õ�DE�ij�����AB�ij������ܸ��ݲ����Ĺ��̰���֪��������δ֪����������ѧ���������������볢����˵һ˵��
����Сӱ�����������ģ���ͼ����֪AB��BD��ED��BD������ֱ�ΪB��D����C��BD�ϣ���BC=CD����A��C��E��һ��ֱ���ϣ���ED=AB��
����˵˵����Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��1�����ԣ���ͼ����֪A��E��B������ͬһֱ���ϣ��ҡ�A=��B=��DEC=90�㣬
��1�����ԣ���ͼ����֪A��E��B������ͬһֱ���ϣ��ҡ�A=��B=��DEC=90�㣬
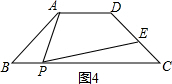 �غϣ�������AP������P��PE��CD�ڵ�E��ʹ�á�APE=��ABC����BPΪ��ֵʱ����EΪCD���е㣮
�غϣ�������AP������P��PE��CD�ڵ�E��ʹ�á�APE=��ABC����BPΪ��ֵʱ����EΪCD���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011���㽭ʡ������ͩ�����п���ѧ��ģ�Ծ��������棩 ���ͣ������
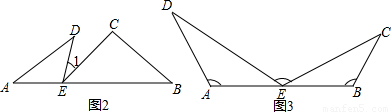
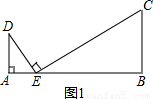
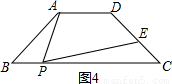
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com