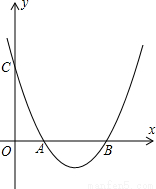
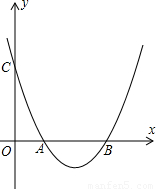
解:(1)易知B(3,0),C(0,3),代入抛物线的解析式中,得:
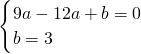
,解得
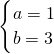
;
∴y=x
2-4x+3.
(2)如图;

∵OB=OC,
∴∠OBC=∠OCB=45°,BC=3

;
易知A(1,0),D(2,-1),
则∠ADP=45°,AD=

,AB=2;
∴∠ABC=∠ADP=45°;
①当点P在x轴上方时,
已知∠APD=∠ACB,则△APD∽△ACB,得:
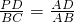
,即
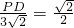
,故PD=3,P(2,2);
②当点P在x轴下方时,此时P′、P关于x轴对称,故P′(2,-2);
因此有两个符合条件的P点,且坐标为P(2,2)或(2,-2).
(3)∵A(1,0),C(0,3),
∴OC=3OA=3;
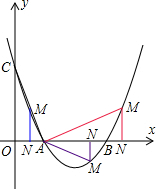
又∠AOC=∠ANM=90°,
若以A、M、N为顶点的三角形与△AOC相似,
则AN=3MN或3AN=MN;
设M(m,m
2-4m+3),则N(m,0);
①当m<1时,AN=1-m,MN=m
2-4m+3;
若AN=3MN,1-m=3(m
2-4m+3),解得m=

,m=1;
若3AN=MN,3(1-m)=m
2-4m+3,解得m=0,m=1;
由于m<1,且m≠0,故上述四个解都不符合题意;
②当1<m<3时,AN=m-1,MN=-(m
2-4m+3);
若AN=3MN,m-1=-3(m
2-4m+3),解得m=1(舍去),m=

;
若3AN=MN,3(m-1)=-(m
2-4m+3),解得m=0(舍去),m=1(舍去);
故M(

,-

);
③当m>3时,AN=m-1,MN=m
2-4m+3;
若AN=3MN,m-1=3(m
2-4m+3),解得m=1(舍去),m=

;
若3AN=MN,3(m-1)=m
2-4m+3,解得m=1(舍去),m=6;
故M(

,

)或(6,5);
综上所述,存在符合条件的M点,且坐标为:M
1(

,

),M
2(6,5),M
3(

,-

).
分析:(1)根据OB=OC,可得到C点的坐标,将B、C的坐标代入抛物线的解析式中,即可求得待定系数的值,从而确定该抛物线的解析式.
(2)根据(1)得到的抛物线的解析式,可求得顶点D的坐标,易求得∠CBO=∠ADP=45°;
当P点在x轴上方时,若∠ACB=∠APD,则△APD∽△ACB,可先求出AB、BC、AD的长,然后根据相似三角形得到的比例线段求出DP的长,从而确定P点的坐标.
当P点在x轴下方时(设为P′),点P′正好和上面所得P点关于x轴对称,由此得解.
(3)此题需要考虑的情况较多,根据A、C的坐标,易知3OA=OC,而∠AOC=∠ANM=90°,若以A、M、N为顶点的三角形与△AOC相似,则:AN=3MN或3AN=MN,可设出点M的横坐标,根据抛物线的解析式表示出它的纵坐标,然后表示出AN、MN的长,进而根据上面两种情况中不同的等量关系求得点M的坐标.(要注意的是,在表示AN、MN的长时,要根据点M的不同位置分类讨论)
点评:此题是二次函数的综合题,主要考查了二次函数解析式的确定以及相似三角形的判定和性质,要注意的是(2)(3)题都需要分类讨论,一定要考虑全面,以免漏解.

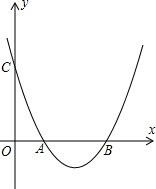 己知抛物线y=ax2-4ax+b与x轴交于A,B两点,(A在B的左侧),与y轴交于C,若OB=OC,且
己知抛物线y=ax2-4ax+b与x轴交于A,B两点,(A在B的左侧),与y轴交于C,若OB=OC,且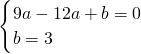 ,解得
,解得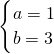 ;
;
 ;
; ,AB=2;
,AB=2;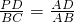 ,即
,即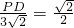 ,故PD=3,P(2,2);
,故PD=3,P(2,2);
 ,m=1;
,m=1; ;
; ,-
,- );
); ;
; ,
, )或(6,5);
)或(6,5); ,
, ),M2(6,5),M3(
),M2(6,5),M3( ,-
,- ).
).

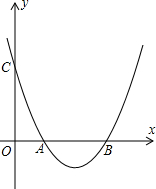 己知抛物线y=ax2-4ax+b与x轴交于A,B两点,(A在B的左侧),与y轴交于C,若OB=OC,且
己知抛物线y=ax2-4ax+b与x轴交于A,B两点,(A在B的左侧),与y轴交于C,若OB=OC,且