
【题目】如图,正方形ABCD的边长为4,M 是AB的中点,且AN=![]() AD,问△CMN是什么三角形?并加以证明。
AD,问△CMN是什么三角形?并加以证明。

【答案】直角三角形;证明过程见解析
【解析】
试题分析:根据题意分别得出AB=BC=CD=AD=4,AM=BM=2,AN=1,DN=3 根据Rt△AMN得出MN的长度,同理得出MC和NC的长度,然后根据勾股定理的逆定理得出直角三角形.
试题解析:三角形CMN是直角三角形
∵正方形ABCD的边长为4 ∴AB=BC=CD=AD=4 ∵M是AB的中点 ∴AM=BM=2 ∵AN= ![]() AD,AD=4
AD,AD=4
∴AN=1,DN=3 ∵在直角三角形AMN中, 满足AM2+AN2=MN2,且AM=2,AN=1 ∴MN= ![]()
同理可得:MC=![]() ,NC=5
,NC=5
∵MN2+MC2=(![]() )2+(
)2+(![]() )2=25,NC2=52=25 ∴MN2+MC2= NC2 ∴三角形CMN是直角三角形。
)2=25,NC2=52=25 ∴MN2+MC2= NC2 ∴三角形CMN是直角三角形。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
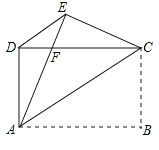
【题目】如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△DEC≌△EDA;(2)求DF的值;(3)在线段AB上找一点P,连结FP使FP⊥AC,连结PC,试判定四边形APCF的形状,并说明理由,直接写出此时线段PF的大小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的![]() ,问橱具店有哪几种进货方案?并说明理由;
,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家环保局统一规定,空气质量分为5级:当空气污染指数达0—50时为1级,质量为优;51—100时为2级,质量为良;101—200时为3级,轻度污染;201—300时为4级,中度污染;300以上时为5级,重度污染.某城市随机抽取了2015年某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:

(1) 本次调查共抽取了 天的空气质量检测结果进行统计;
(2) 补全条形统计图;
(3) 扇形统计图中3级空气质量所对应的圆心角为 °;
(4) 如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计2015年该城市有多少天不适宜开展户外活动.(2015年共365天)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【知识生成】我们已经知道,通过不同的方法表示同一图形的面积,可以探求相应的等式.
2002年8月在北京召开了国际数学大会,大会会标如图1所示,它是由四个形状大小完全相同的直角三角形与中间的小正方形拼成的一个大正方形.直角三角形的两条直角边长分别为a、b ,斜边长为c.
(1)图中阴影部分的面积用两种方法可分别表示为 、 ;
(2)你能得出的a, b, c之间的数量关系是 (等号两边需化为最简形式);
(3)若一直角三角形的两条直角边长为5和12, 则其斜边长为 .

【知识迁移】通过不同的方法表示同一几何体的体积,也可以探求相应的等式.
如图2是边长为![]() 的正方体,被如图所示的分割线分成8块.
的正方体,被如图所示的分割线分成8块.
(4)用不同的方法计算这个正方体的体积,就可以得到一个等式,这个等式可以为 ;
(5)已知![]() ,
, ![]() ,利用上面的规律求
,利用上面的规律求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com