
【题目】已知:a、b、c是△ABC的三边长,化简 ![]() .
.
【答案】解:∵a、b、c是△ABC的三边长, ∴a+b>c,b+c>a,b+a>c,
∴原式=|a+b+c|﹣|b+c﹣a|+|c﹣b﹣a|
=a+b+c﹣(b+c﹣a)+(b+a﹣c)
=a+b+c﹣b﹣c+a+b+a﹣c
=3a+b﹣c.
【解析】根据三角形的三边关系定理得出a+b>c,b+c>a,b+a>c,根据二次根式的性质得出含有绝对值的式子,最后去绝对值符号后合并即可.
【考点精析】本题主要考查了二次根式的性质与化简和三角形三边关系的相关知识点,需要掌握1、如果被开方数是分数(包括小数)或分式,先利用商的算数平方根的性质把它写成分式的形式,然后利用分母有理化进行化简.2、如果被开方数是整数或整式,先将他们分解因数或因式,然后把能开得尽方的因数或因式开出来;三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到的△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( )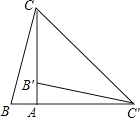
A.32°
B.64°
C.77°
D.87°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC, ①如图1,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+ ![]() ∠A;
∠A;
②如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°﹣∠A;
③如图3,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°﹣ ![]() ∠A.
∠A.
上述说法正确的个数是( )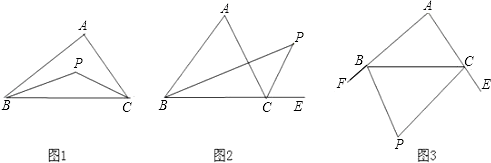
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为:「P」,即「P」=|x|+|y|.
(1)求点A(﹣1,3)的勾股值「A」;
(2)若点B在第一象限且满足「B」=3,求满足条件的所有B点与坐标轴围成的图形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com