Question

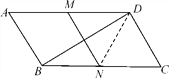
【题目】如图，在平行四边形ABCD中，∠C＝60°，M、N分别是AD、BC的中点，BC＝2CD.

(1)求证：四边形MNCD是平行四边形；

(2)求证：BD＝MN.

Answer 1

【答案】见解析

【解析】试题分析：（1）要证明四边形MNCD是平行四边形，即要证明MD＝NC，MD∥NC，由四边形ABCD是平行四边形可得AD＝BC，AD∥BC，又因为M、N分别是AD、BC的中点，所以MD＝NC，MD∥NC；（2）连结ND，由四边形MNCD是平行四边形可得 MN＝DC，因为N是BC的中点，所以BN＝CN，结合BC＝2CD，∠C＝60°可以得出△NCD是等边三角形，进而得出ND＝NC，∠DNC＝60°，由三角形外角的性质可得∠NBD＋∠NDB＝∠DNC，

因为DN＝NC＝NB，所以∠DBN＝∠BDN＝∠DNC＝30°，所以∠BDC＝90°，最后结合tan∠DBC可证明DB＝MN.

试题解析：

(1)∵四边形ABCD是平行四边形，∴AD＝BC，AD∥BC，

∵M、N分别是AD、BC的中点，∴MD＝NC，MD∥NC，

∴四边形MNCD是平行四边形；　

(2)连结ND，

∵四边形MNCD是平行四边形，∴MN＝DC，

∵N是BC的中点，∴BN＝CN，

∵BC＝2CD，∠C＝60°，∴△NCD是等边三角形，∴ND＝NC，∠DNC＝60°，

∵∠DNC是△BND的外角，∴∠NBD＋∠NDB＝∠DNC，

∵DN＝NC＝NB，∴∠DBN＝∠BDN＝∠DNC＝30°，∴∠BDC＝90°，

∵tan∠DBC＝tan30°＝＝，

∴DB＝DC＝MN.