
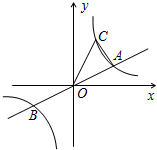
 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=$\frac{k}{x}$上一点,且点C在直线y=$\frac{1}{2}$x的上方.
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=$\frac{k}{x}$上一点,且点C在直线y=$\frac{1}{2}$x的上方.分析 (1)利用待定系数法即可解决.
(2)过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,根据S△AOC=S△COF+S梯形ACFE-S△AOE=6,列出方程即可解决.
解答 解:(1)∵点B(-4,-2)在双曲线y=$\frac{k}{x}$上,
∴$\frac{k}{-4}$=-2,
∴k=8,
∴双曲线的函数解析式为y=$\frac{8}{x}$.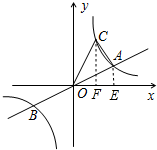
(2)过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,
∵正比例函数与反比例函数的交点A、B关于原点对称,
∴A(4,2),∴OE=4,AE=2,
设点C的坐标为(a,$\frac{8}{a}$),则OF=a,CF=$\frac{8}{a}$,
则S△AOC=S△COF+S梯形ACFE-S△AOE,
=$\frac{1}{2}$×$a×\frac{8}{a}$+$\frac{1}{2}$(2+$\frac{8}{a}$)(4-a)-$\frac{1}{2}$×4×2
=$\frac{16-{a}^{2}}{a}$,
∵△AOC的面积为6,
∴$\frac{16-{a}^{2}}{a}$=6,
整理得a2+6a-16=0,
解得a=2或-8(舍弃),
∴点C的坐标为(2,4).
点评 本题考查反比例函数与一次函数交点、解题的关键是熟练掌握待定系数法,学会利用分割法求四边形面积,学会用方程的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
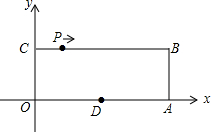 如图,平面直角坐标系xOy中,点O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
如图,平面直角坐标系xOy中,点O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{a-b}$ | B. | $\frac{b}{a-b}$ | ||
| C. | $\frac{{a}^{2}+ab+2{b}^{2}}{{a}^{2}-{b}^{2}}$ | D. | $\frac{{a}^{2}+ab+{b}^{2}}{{a}^{2}-{b}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 数学课上,老师要求同学们画函数y=|x|的图象,小红联想绝对值的性质得y=x(x≥0)或y=-x(x≤0),于是她很快作出了该函数的图象(如图),和你的同桌交流一下,小红的作法对吗?如果不对,试画出该函数的图象.
数学课上,老师要求同学们画函数y=|x|的图象,小红联想绝对值的性质得y=x(x≥0)或y=-x(x≤0),于是她很快作出了该函数的图象(如图),和你的同桌交流一下,小红的作法对吗?如果不对,试画出该函数的图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com