C
分析:先根据题意画出图形,再根据线段垂直平分线及直角三角形的性质得出∠BAD、∠B、∠DAC之间的关系,列出方程即可求解.
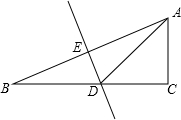
解答:如图所示:Rt△ABC中,DE是AB的垂直平分线,∠B=2∠DAC,
∵△ABC是直角三角形,
∴∠B+∠BAC=90°,
∵DE是AB的垂直平分线,
∴∠B=∠BAD,
∵∠B=2∠DAC,
∴∠BAD=2∠DAC,
设∠DAC=x,则∠BAD=∠B=2x,
∴∠BAD+∠B+∠DAC=2x+2x+x=5x=90°,
∴x=18°,
∴∠B=18°×2=36°.
故选C.
点评:本题考查的是线段垂直平分线的性质,解答此题的关键是根据题意画出图形,再利用方程的思想求解.




 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案