如上图.设四边形ABCD是边长为1的正方形.以对角线AC为边作第二个正方形ACEF.再以对角线AE为边作笫三个正方形AEGH.如此下去-．若正方形ABCD的边长记为a1.按上述方法所作的正方形的边长依次为a2.a3.a4.-.an.则an= ．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

如上图，设四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作笫三个正方形AEGH，如此下去…．若正方形ABCD的边长记为a1，按上述方法所作的正方形的边长依次为a2，a3，a4，…，an，则an= ．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：2014-2015学年河南省平顶山市中考二模数学试卷（解析版） 题型：选择题

如图，△ABC中，∠ACB=90°，∠A=30°，AB=16．点P是斜边AB上一点．过点P作PQ⊥AB，垂足为P，交边AC（或边CB）于点Q，设AP=x，△APQ的面积为y，则y与x之间的函数图象大致为（）

查看答案和解析>>

科目：初中数学 来源：2015-2016学年江苏省八年级上学期第一次月考数学试卷（解析版） 题型：解答题

如图，在平面直角坐标系xOy中，点A的坐标为（﹣2，0），等边三角形AOC经过平移或轴对称都可以得到△．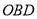

（1）△沿x轴向右平移得到△，则平移的距离是个单位长度；△与△关于直线对称，则对称轴是；

（2）连结AD，交OC于点E，求∠AEO的度数．

查看答案和解析>>

科目：初中数学 来源：2015-2016学年江苏省八年级上学期第一次月考数学试卷（解析版） 题型：选择题

下列运算结果正确的是（）

A．2a3•a4b=2a12b B．（a4）3=a7

C．（3a）3=3a3 D．a（a+1）=a2+a

查看答案和解析>>

科目：初中数学 来源：2016届辽宁省九年级上学期10月月考数学试卷（解析版） 题型：解答题

（本题12分）某百货大搂服装柜在销售中发现：“宝乐”牌童装平均每天可售出20件，每件盈利40元．为了迎接“十·一”国庆节，商场决定采取适当的降价措施，扩大销售量，增加盈利，减少库存．经市场调查发现：如果每件童装降价4元，那么平均每天就可多售出8件．要想平均每天销售这种童装盈利1200元，那么每件童装应降价多少元？平均每天的销售量是多少件？

查看答案和解析>>

科目：初中数学 来源：2016届辽宁省九年级上学期10月月考数学试卷（解析版） 题型：填空题

关于的方程是一元二次方程，则______．