
分析 (1)根据两点间距离公式即可得到结论;
(2)利用两点间距离公式求$\sqrt{{x}^{2}+4}$+$\sqrt{(3-x)^{2}+36}$+1的最小值,本题可以化归为:在x轴上找一点P(x,0),使其与两定点A(0,2),B(3,6)的距离之和为最小,然后根据两点间距离公式即可得到结论.
解答 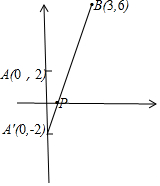 解:(1)∵P(-2,7),Q(3,-5),
解:(1)∵P(-2,7),Q(3,-5),
∴PQ=$\sqrt{(-2-3)^{2}+(7+5)^{2}}$=13;
(2)如图,利用两点间距离公式求$\sqrt{{x}^{2}+4}$+$\sqrt{(3-x)^{2}+36}$+1的最小值,
本题可以化归为:在x轴上找一点P(x,0),
使其与两定点A(0,2),B(3,6)的距离之和为最小,
即$\sqrt{(x-0)^{2}+(0-2)^{2}}$+$\sqrt{(x-3)^{2}+(0-6)^{2}}$有最小值.
作A点关于x轴的对称点A'(0,-2),连接BA',与x轴的交点即为所求的P点.
此时$\sqrt{{x}^{2}+4}$+$\sqrt{(3-x)^{2}+36}$有最小值,
其最小值=A′B=$\sqrt{(0-3)^{2}+(-2-6)^{2}}$=$\sqrt{73}$.
∴$\sqrt{{x}^{2}+4}$+$\sqrt{(3-x)^{2}+36}$+1的最小值=$\sqrt{73}$+1.
点评 本题考查了轴对称-最小距离问题,两点间的距离公式,正确的理解题意是解题的关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,四边形ABDC中,∠B=∠D=90°,BC=AB,以AB为直径的⊙O交BC于E.
如图,四边形ABDC中,∠B=∠D=90°,BC=AB,以AB为直径的⊙O交BC于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
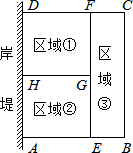 为了节省材料,某水产养殖户利用水库的岸堤(岸堤长15m)为一边,用总长为80m的栅栏围在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为y m2.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤长15m)为一边,用总长为80m的栅栏围在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为y m2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
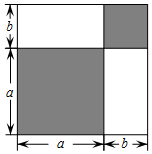 请认真观察图形,解答下列问题:
请认真观察图形,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com