
【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
【答案】(1)28;(2)![]() ;(3)当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形;
;(3)当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形;
【解析】
(1)根据点P、Q的运动速度求出AP,再求出BP和BQ,用勾股定理求得PQ即可;
(2)设出发t秒钟后,△PQB能形成等腰三角形,则BP=BQ,由BQ=2t,BP=8-t,列式求得t即可;
(3)当点Q在边CA上运动时,能使△BCQ成为等腰三角形的运动时间有三种情况:
①当CQ=BQ时,则∠C=∠CBQ,可证明∠A=∠ABQ,则BQ=AQ,则CQ=AQ,从而求得t;
②当CQ=BC时,则BC+CQ=12,易求得t;
③当BC=BQ时,过B点作BE⊥AC于点E,则求出BE,CE,即可得出t.
解:(1)∵BQ=2×2=4(cm),
BP=AB﹣AP=16﹣2×1=14(cm ),
∵∠B=90°,
∴S△PBQ=![]() ;
;
(2)BQ=2t,BP=16﹣t,
根据题意得:2t=16﹣t,
解得:t=![]() ,
,
即出发![]() 秒钟后,△PQB能形成等腰三角形;
秒钟后,△PQB能形成等腰三角形;
(3)①当CQ=BQ时,如图1所示,
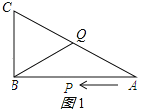
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°.
∠A+∠C=90°,
∴∠A=∠ABQ,
∴BQ=AQ,
∴CQ=AQ=10,
∴BC+CQ=22,
∴t=22÷2=11秒.
②当CQ=BC时,如图2所示,
则BC+CQ=24,
∴t=24÷2=12秒.

③当BC=BQ时,如图3所示,
过B点作BE⊥AC于点E,
则BE=![]() =
=![]() ,
,

∴CE=![]() =
=![]() =
=![]() ,
,
∴CQ=2CE=14.4,
∴BC+CQ=26.4,
∴t=26.4÷2=13.2秒.
综上所述:当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=6,E是BA延长线的一点,P是∠EAC的平分线上一个动点,当△APC是以AC为腰的等腰三角形时,△APC的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉市光谷实验中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),下列说法错误的是( )

A. 九(1)班的学生人数为40 B. m的值为10
C. n的值为20 D. 表示“足球”的扇形的圆心角是70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力,增强保护汉子的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为![]() (分),且
(分),且![]() ,将其按分数段分为五组,绘制出以下不完整表格:
,将其按分数段分为五组,绘制出以下不完整表格:
组别 | 成绩 | 频数(人数) | 频率 |
一 |
| 2 | 0.04 |
二 |
| 10 | 0.2 |
三 |
| 14 | b |
四 |
| a | 0.32 |
五 |
| 8 | 0.16 |
(1)本次决赛共有 名学生参加;
(2)直接写出表中a= ,b= ;
(3)请补全下面相应的频数分布直方图;

(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣4,0),点B的坐标是(0,b)(b>0).P是直线AB上的一个动点,作PC⊥x轴,垂足为C.记点P关于y轴的对称点为P′(点P′不在y轴上),连接PP′,P′A,P′C.设点P的横坐标为a. 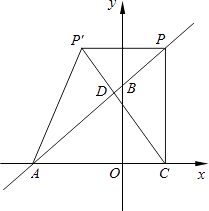
(1)当b=3时, ①求直线AB的解析式;
②若点P′的坐标是(﹣1,m),求m的值;
(2)若点P在第一象限,记直线AB与P′C的交点为D.当P′D:DC=1:3时,求a的值;
(3)是否同时存在a,b,使△P′CA为等腰直角三角形?若存在,请求出所有满足要求的a,b的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是⊙O的直径,弦AB⊥CD,垂足为点M,AB=20,分别以CM、DM为直径作两个大小不同的 ⊙O1和⊙O2 , 则图中阴影部分的面积为(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
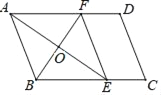
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于E,点F在AD上,且AF=AB,连接EF.
(1)判断四边形ABEF的形状并证明;
(2)若AE、BF相交于点O,且四边形ABEF的周长为20,BF=6,求AE的长度及四边形ABEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如下三个函数图象中,有两个函数图象能近似地刻画如下![]() 两个情境:
两个情境:
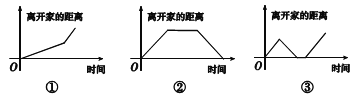
情境![]() :小芳离开家不久,发现把作业本忘在家里,于是返回家里找到了作业本再去学校;
:小芳离开家不久,发现把作业本忘在家里,于是返回家里找到了作业本再去学校;
情境![]() :小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
(1)情境![]() ,
, ![]() 所对应的函数图象分别为 , (填写序号).
所对应的函数图象分别为 , (填写序号).
(2)请你为剩下的函数图象写出一个适合的情境.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com