
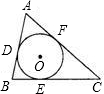
 如图所示,⊙O分别切△ABC的三边AB,BC,CA于点D,E,F,若BC=a,AC=b,AB=c.
如图所示,⊙O分别切△ABC的三边AB,BC,CA于点D,E,F,若BC=a,AC=b,AB=c.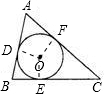
 ,
, ,
, ,BE=
,BE= ,CF=
,CF= .
.
 .
.

科目:初中数学 来源: 题型:
 要对一块长60米、宽40米的矩形荒地ABCD进行绿化和硬化.
要对一块长60米、宽40米的矩形荒地ABCD进行绿化和硬化.| 1 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
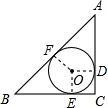
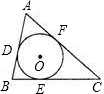 如图所示,⊙O分别切△ABC的三边AB,BC,CA于点D,E,F,若BC=a,AC=b,AB=c.
如图所示,⊙O分别切△ABC的三边AB,BC,CA于点D,E,F,若BC=a,AC=b,AB=c.查看答案和解析>>
科目:初中数学 来源: 题型:
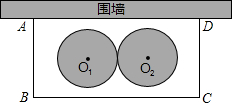 某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABCD.已知木栏总长为120米,设AB边的长为x米,长方形ABCD的面积为S平方米.
某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABCD.已知木栏总长为120米,设AB边的长为x米,长方形ABCD的面积为S平方米.查看答案和解析>>
科目:初中数学 来源:《第24章 圆》2009年习题课(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com