
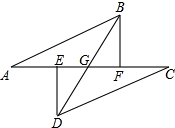
 如图,已知AE=CF,AB=CD,DE⊥AC,BF⊥AC,求证:BD平分EF.
如图,已知AE=CF,AB=CD,DE⊥AC,BF⊥AC,求证:BD平分EF.
|
|


科目:初中数学 来源: 题型:
 按照下列要求完成作图及相应的问题解答
按照下列要求完成作图及相应的问题解答查看答案和解析>>
科目:初中数学 来源: 题型:
 黄岩岛是我国南沙群岛的一个小岛,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并立即返航,渔政船接到报告后,立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离;和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)
黄岩岛是我国南沙群岛的一个小岛,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并立即返航,渔政船接到报告后,立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离;和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com