
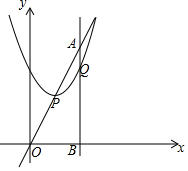
 如图,点A(2,4),作AB⊥x铀于点B,抛物线y=x2+bx+c的顶点P在直线OA上,且抛物线交线段AB于点Q,求线段AQ的最大值及此时抛物线的解析式.
如图,点A(2,4),作AB⊥x铀于点B,抛物线y=x2+bx+c的顶点P在直线OA上,且抛物线交线段AB于点Q,求线段AQ的最大值及此时抛物线的解析式. 分析 先求得直线OA的解析式,根据顶点P在直线OA上,设出点P的坐标,根据顶点坐标的公式得出b与c的关系,根据点Q的横坐标为2,代入抛物线即可得出点Q的纵坐标.
解答 解:设直线OA的解析式为y=kx,
把A(2,4)代入得y=2x,
∵抛物线y=x2+bx+c的顶点为点P,
∴设点P(-$\frac{b}{2}$,$\frac{4c-{b}^{2}}{4}$),
∵点P在直线OA上,
∴2×(-$\frac{b}{2}$)=$\frac{4c-{b}^{2}}{4}$,
∴c=$\frac{{b}^{2}-4b}{4}$,
∵点Q的横坐标为2,
∴y=4+2b+c,
将c=$\frac{{b}^{2}-4b}{4}$代入得,y=4+2b+$\frac{{b}^{2}-4b}{4}$,
∴Q(2,4+2b+$\frac{{b}^{2}-4b}{4}$)
∴AQ=4-(4+2b+$\frac{{b}^{2}-4b}{4}$),
整理得AQ=-$\frac{1}{4}$b2-b,
∴当b=-$\frac{-1}{2×(-\frac{1}{4})}$=-2时,AQ最长=$\frac{-1}{4×(-\frac{1}{4})}$=1,
当b=1时,c=-$\frac{3}{4}$,
∴此时抛物线的解析式为y=x2+x-$\frac{3}{4}$.
点评 本题考查了用待定系数法求二次函数的解析式,掌握二次函数顶点坐标的求法是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1-a>1-b | B. | $\frac{1}{a}<\frac{1}{b}$ | C. | $\frac{a}{b}<1$ | D. | $-\frac{1}{3}a>-\frac{1}{3}b$. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=$\frac{1}{2}$x2-x-4与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,过点C作直线1∥x轴.将该抛物线在y轴左侧的部分沿直线1翻折,抛物线的其余部分保持不变.得到一个新的图象,记为G.请你结合图象问答:当直线y=$\frac{1}{2}$x+b与图象G只有一个公共点时,求b的取值范围.
已知抛物线y=$\frac{1}{2}$x2-x-4与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,过点C作直线1∥x轴.将该抛物线在y轴左侧的部分沿直线1翻折,抛物线的其余部分保持不变.得到一个新的图象,记为G.请你结合图象问答:当直线y=$\frac{1}{2}$x+b与图象G只有一个公共点时,求b的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
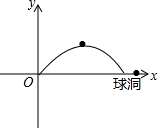 如图,老童在一次高尔夫球的练习中,在原点O处击球,球的飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{8}{5}$x,其中y表示球飞行的高度(单位:米),x表示球飞行的水平距离(单位:米),结果球的落地点离球洞2米(击球点、落地点、球洞三点共线).
如图,老童在一次高尔夫球的练习中,在原点O处击球,球的飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{8}{5}$x,其中y表示球飞行的高度(单位:米),x表示球飞行的水平距离(单位:米),结果球的落地点离球洞2米(击球点、落地点、球洞三点共线).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
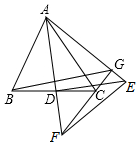 如图,△ABC是边长为6的等边三角形,过点A作边BC的垂线,垂足为点D,将△ADC绕着点D旋转得列△DEF(其中点A的对应点为点E,点C的对应点为点F),直线AE,FC相交于点G,连接BG,设BG=y,在旋转过程中,y的最大值是3+3$\sqrt{3}$.
如图,△ABC是边长为6的等边三角形,过点A作边BC的垂线,垂足为点D,将△ADC绕着点D旋转得列△DEF(其中点A的对应点为点E,点C的对应点为点F),直线AE,FC相交于点G,连接BG,设BG=y,在旋转过程中,y的最大值是3+3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com