
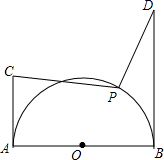
 如图,半圆的半径为1,AB为直径,AC、BD为切线,AC=1,BD=2,P为$\widehat{AB}$上一动点,求$\frac{\sqrt{2}}{2}$PC+PD的最小值.
如图,半圆的半径为1,AB为直径,AC、BD为切线,AC=1,BD=2,P为$\widehat{AB}$上一动点,求$\frac{\sqrt{2}}{2}$PC+PD的最小值. 分析 如图当A、P、D共线时,$\frac{\sqrt{2}}{2}$PC+PD最小,根据$\frac{\sqrt{2}}{2}$PC+PD=PM+PD=DM=AD-AM即可计算.
解答 解:如图当A、P、D共线时,$\frac{\sqrt{2}}{2}$PC+PD最小.
理由:连接PB、CO,AD与CO交于点M,
∵AB=BD=4,BD是切线,
∴∠ABD=90°,∠BAD=∠D=45°,
∵AB是直径,
∴∠APB=90°,
∴∠PAB=∠PBA=45°,
∴PA=PB,PO⊥AB,
∵AC=PO=2,AC∥PO,
∴四边形AOPC是平行四边形,
∴OA=OP,∠AOP=90°,
∴四边形AOPC是正方形,
∴PM=$\frac{\sqrt{2}}{2}$PC,
∴$\frac{\sqrt{2}}{2}$PC+PD=PM+PD=DM,
∵DM⊥CO,
∴此时$\frac{\sqrt{2}}{2}$PC+DP最小=AD-AM=4$\sqrt{2}$-$\sqrt{2}$=3$\sqrt{2}$.
点评 本题考查切线的性质、轴对称-最短问题、正方形的判定和性质、等腰直角三角形的判定和性质等知识,解题的关键是找到点P的位置,学会通过特殊点探究问题,找到解题的突破口,属于中考常考题型.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
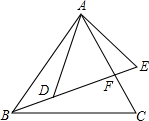 如图,点B、D、E在一条直线上,BE与AC相交于点F,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,若∠EAC=18°,则∠EBC=18°.
如图,点B、D、E在一条直线上,BE与AC相交于点F,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,若∠EAC=18°,则∠EBC=18°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 太阳从西方升起 | B. | 打开电视正在播放《新闻联播》 | ||
| C. | 若a≤0,则|a|=-a | D. | 某运动员投篮时连续3次全中 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
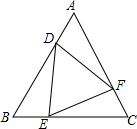 如图,点D、E、F分别是边长为6的等边三角形ABC边AB、BC、AC上的点,且AD=BE=CF.
如图,点D、E、F分别是边长为6的等边三角形ABC边AB、BC、AC上的点,且AD=BE=CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com