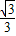练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    根据tan30°=构造△ABC，使∠A=30°，AB=2，BC=1，AC=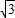，再延长CA到点D，使AB=AD，连接BD，则tan15°=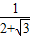=2-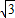，同样根据tan45°=1，模仿前面的做法求出tan22.5°的值．
    【答案】分析：利用正切值等于对边比邻边，构造直角三角形求解．
    解答：解：作∠A=45°，AB=，AC=BC=1，
    延长CA至点D，使AD=AB，连接BD．
    则tanD=tan22.5°==-1．
    点评：本题是信息题，由题中给出求tan15°的方法，构造出能求tan22.5°的值的直角三角形求解，关键构造出△BAD是等腰三角形，而∠BAC为45°，又为△BAD的外角，所以∠D=22.5，再由正切的定义求出tan22.5°的值．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：第1章《解直角三角形》中考题集（11）：1.1 锐角三角函数（解析版） 题型：解答题

    阅读以下材料：
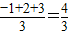    对于三个数a、b、c，用M（a，b，c）表示这三个数的平均数，用min（a，b，c）表示这三个数中最小的数．例如：M{-1，2，3}=；min{-1，2，3}=-1；min{-1，2，a}=a（a≤-1）；-1（a＞-1）
    解决下列问题：
    （1）填空：min{sin30°，cos45°，tan30°}=______，如果min{2，2x+2，4-2x}=2，则x的取值范围为______≤x≤______；
    （2）①如果M{2，x+1，2x}=min{2，x+1，2x}，求x．
    ②根据①，你发现了结论“如果M{a，b，c}=min{a，b，c}，那么______（填a，b，c的大小关系）”，
    证明你发现的结论．
    ③运用②的结论，填空：若M{2x+y+2，x+2y，2x-y}=min{2x+y+2，x+2y，2x-y}，则x+y=______；
    （3）在同一直角坐标系中作出函数y=x+1，y=（x+1）2，y=2-x的图象（不需列表描点），通过观察图象，填空：min{x+1，（x-1）2，2-x}的最大值为______．

    查看答案和解析>>

    科目：初中数学 来源：第25章《解直角三角形》中考题集（11）：25.2 锐角的三角函数值（解析版） 题型：解答题

    阅读以下材料：
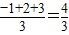    对于三个数a、b、c，用M（a，b，c）表示这三个数的平均数，用min（a，b，c）表示这三个数中最小的数．例如：M{-1，2，3}=；min{-1，2，3}=-1；min{-1，2，a}=a（a≤-1）；-1（a＞-1）
    解决下列问题：
    （1）填空：min{sin30°，cos45°，tan30°}=______，如果min{2，2x+2，4-2x}=2，则x的取值范围为______≤x≤______；
    （2）①如果M{2，x+1，2x}=min{2，x+1，2x}，求x．
    ②根据①，你发现了结论“如果M{a，b，c}=min{a，b，c}，那么______（填a，b，c的大小关系）”，
    证明你发现的结论．
    ③运用②的结论，填空：若M{2x+y+2，x+2y，2x-y}=min{2x+y+2，x+2y，2x-y}，则x+y=______；
    （3）在同一直角坐标系中作出函数y=x+1，y=（x+1）2，y=2-x的图象（不需列表描点），通过观察图象，填空：min{x+1，（x-1）2，2-x}的最大值为______．

    查看答案和解析>>

    科目：初中数学 来源：2009-2010学年九年级（上）期末数学全册内容检测试卷（解析版） 题型：解答题

    阅读以下材料：
    对于三个数a、b、c，用M（a，b，c）表示这三个数的平均数，用min（a，b，c）表示这三个数中最小的数．例如：M{-1，2，3}=；min{-1，2，3}=-1；min{-1，2，a}=a（a≤-1）；-1（a＞-1）
    解决下列问题：
    （1）填空：min{sin30°，cos45°，tan30°}=______，如果min{2，2x+2，4-2x}=2，则x的取值范围为______≤x≤______；
    （2）①如果M{2，x+1，2x}=min{2，x+1，2x}，求x．
    ②根据①，你发现了结论“如果M{a，b，c}=min{a，b，c}，那么______（填a，b，c的大小关系）”，
    证明你发现的结论．
    ③运用②的结论，填空：若M{2x+y+2，x+2y，2x-y}=min{2x+y+2，x+2y，2x-y}，则x+y=______；
    （3）在同一直角坐标系中作出函数y=x+1，y=（x+1）2，y=2-x的图象（不需列表描点），通过观察图象，填空：min{x+1，（x-1）2，2-x}的最大值为______．

    查看答案和解析>>

    科目：初中数学 来源：2008年全国中考数学试题汇编《锐角三角函数》（04）（解析版） 题型：解答题

    （2008•镇江）阅读以下材料：
    对于三个数a、b、c，用M（a，b，c）表示这三个数的平均数，用min（a，b，c）表示这三个数中最小的数．例如：M{-1，2，3}=；min{-1，2，3}=-1；min{-1，2，a}=a（a≤-1）；-1（a＞-1）
    解决下列问题：
    （1）填空：min{sin30°，cos45°，tan30°}=______，如果min{2，2x+2，4-2x}=2，则x的取值范围为______≤x≤______；
    （2）①如果M{2，x+1，2x}=min{2，x+1，2x}，求x．
    ②根据①，你发现了结论“如果M{a，b，c}=min{a，b，c}，那么______（填a，b，c的大小关系）”，
    证明你发现的结论．
    ③运用②的结论，填空：若M{2x+y+2，x+2y，2x-y}=min{2x+y+2，x+2y，2x-y}，则x+y=______；
    （3）在同一直角坐标系中作出函数y=x+1，y=（x+1）2，y=2-x的图象（不需列表描点），通过观察图象，填空：min{x+1，（x-1）2，2-x}的最大值为______．

    查看答案和解析>>

    同步练习册答案