Question

已知⊙O₁和⊙O₂外切于一点，AB是外切公切线，A、B是切点，如果AB=6，直线AB与O₁O₂所夹的角为30°，则两圆的半径分别是________．

Answer 1

，3
分析：根据题意画出图形，过点O₁作O₂B的垂线，得到∠CO₁O₂=30°，可以求出大圆半径是小圆半径的3倍，然后在直角△O₁CO₂中用勾股定理计算可以求出两个圆的半径．
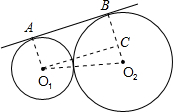
解答：解：根据题意画出图形，如图：
连接O₁A，O₂B，
∵AB是两圆的外公切线，
∴O₁A⊥AB，O₂B⊥AB，
连接O₁O₂，过点O₁作O₁C⊥O₂B，
则：O₁C=AB，∠CO₁O₂=30°，
设⊙O₁的半径为r，⊙O₂的半径为R，
在直角△O₁CO₂中，CO₂=O₁O₂，
即：R+r=2（R-r）
得到：R=3r．
∴由O₁O₂²=O₁C²+O₂C²得到：
（4r）²=36+（2r）²
解得：r=，
∴R=3．
所以两圆的半径分别是：，3．
故答案是：，3．
点评：本题考查的是圆与圆的位置关系，根据两圆外切得到圆心距等于两半径的和，然后由外公切线，过O₁作O₂B的垂线，得到直角三角形，在直角三角形中用勾股定理计算求出两圆的半径．