
 已知:如图所示,直线y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$交x轴于点A,交y轴于点B,若点P从点A出发,沿射线AB作匀速运动,点Q从点B出发,沿射线BO作匀速直线运动,两点同时出发,运动速度也相同,当△BPQ为直角三角形时,则点Q的坐标为(0,$\frac{\sqrt{3}}{3}$)或(0,-$\frac{\sqrt{3}}{3}$).
已知:如图所示,直线y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$交x轴于点A,交y轴于点B,若点P从点A出发,沿射线AB作匀速运动,点Q从点B出发,沿射线BO作匀速直线运动,两点同时出发,运动速度也相同,当△BPQ为直角三角形时,则点Q的坐标为(0,$\frac{\sqrt{3}}{3}$)或(0,-$\frac{\sqrt{3}}{3}$). 分析 根据题意表示出△BPQ的三边长,分∠BQP=90°、∠QBP=90°、∠BPQ=90°三种情况,根据勾股定理计算.
解答 解:对于直线y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$,
当y=0时,即-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$=0,
解得,x=3,
当x=0时,y=$\sqrt{3}$,
∴OA=3,OB=$\sqrt{3}$,
∴∠OAB=30°,
设运动的速度为1,时间为t,
则点P的坐标为:(3-$\frac{\sqrt{3}}{2}$t,$\frac{1}{2}$t),点Q的坐标为:(0,$\sqrt{3}$-t),
则BQ=t,PB=2$\sqrt{3}$-t,PQ=$\sqrt{(3-\frac{\sqrt{3}}{2}t)^{2}+(\frac{3}{2}t-\sqrt{3})^{2}}$,
当∠BPQ=90°时,(2$\sqrt{3}$-t)2+(3-$\frac{\sqrt{3}}{2}$t)2+($\frac{3}{2}$t-$\sqrt{3}$)2=t2,
解得,t1=2$\sqrt{3}$,t2=$\frac{4\sqrt{3}}{3}$,
点Q的坐标为(0,-$\frac{\sqrt{3}}{3}$).,
当∠BQP=90°时,t2+(3-$\frac{\sqrt{3}}{2}$t)2+($\frac{3}{2}$t-$\sqrt{3}$)2=(2$\sqrt{3}$-t)2,
解得,t1=0,t2=$\frac{2\sqrt{3}}{3}$,
则点Q的坐标为(0,$\frac{\sqrt{3}}{3}$),
当∠PBQ=90°时,t2+(2$\sqrt{3}$-t)2=(3-$\frac{\sqrt{3}}{2}$t)2+($\frac{3}{2}$t-$\sqrt{3}$)2,
解得,t1=0,t2=2$\sqrt{3}$,
点Q与B重合,
故答案为:(0,$\frac{\sqrt{3}}{3}$)或(0,-$\frac{\sqrt{3}}{3}$).
点评 本题考查的是一次函数图象上点的坐标特征,灵活运用分情况讨论思想、掌握两点间的距离公式是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
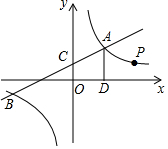 如图,一次函数y1=k1x+2与反比例函数${y_2}=\frac{k_2}{x}$的图象交于点A(4,m)和B(-8,-2),与y轴交于点C.
如图,一次函数y1=k1x+2与反比例函数${y_2}=\frac{k_2}{x}$的图象交于点A(4,m)和B(-8,-2),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
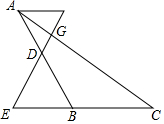 如图,在△ABC中,D是AB的中点,点E在CB的延长线上,AF∥BC,交ED的延长线于点F,EF交AC于点G,若CG:GA=3:1,BC=8,求AF的长.
如图,在△ABC中,D是AB的中点,点E在CB的延长线上,AF∥BC,交ED的延长线于点F,EF交AC于点G,若CG:GA=3:1,BC=8,求AF的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com