
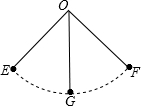
 如图,一条细绳系着一个小球在平面内摆动,已知细绳从悬挂点O到球心的长度OG为50厘米,小球在左、右两个最高位置时(不考虑阻力等其他因素),细绳相应所成的角90°.
如图,一条细绳系着一个小球在平面内摆动,已知细绳从悬挂点O到球心的长度OG为50厘米,小球在左、右两个最高位置时(不考虑阻力等其他因素),细绳相应所成的角90°.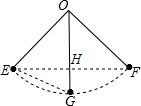 解:(1)连接EF交OG于点H,
解:(1)连接EF交OG于点H, cm,
cm, (cm);
(cm); ,HG=50-25
,HG=50-25 ,
,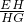 =
=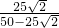 =
= -1.
-1.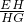 即可得出结论.
即可得出结论.

科目:初中数学 来源: 题型:
 15、如图,一条细绳系着一个小球在平面内摆动、已知细绳的长度为20厘米,当小球摆动到最高位置时,细绳偏转的角度为28°,那么小球在最高位置与最低位置时的高度差为
15、如图,一条细绳系着一个小球在平面内摆动、已知细绳的长度为20厘米,当小球摆动到最高位置时,细绳偏转的角度为28°,那么小球在最高位置与最低位置时的高度差为查看答案和解析>>
科目:初中数学 来源: 题型:
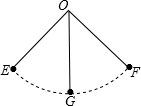 (2013•嘉定区一模)如图,一条细绳系着一个小球在平面内摆动,已知细绳从悬挂点O到球心的长度OG为50厘米,小球在左、右两个最高位置时(不考虑阻力等其他因素),细绳相应所成的角90°.
(2013•嘉定区一模)如图,一条细绳系着一个小球在平面内摆动,已知细绳从悬挂点O到球心的长度OG为50厘米,小球在左、右两个最高位置时(不考虑阻力等其他因素),细绳相应所成的角90°.查看答案和解析>>
科目:初中数学 来源:2013年上海市嘉定区中考数学一模试卷(解析版) 题型:解答题
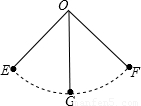
查看答案和解析>>
科目:初中数学 来源:2009年上海市宝山区中考数学一模试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com