
如图,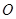 是直线
是直线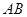 上的点,
上的点,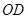 是
是 的平分线,
的平分线,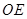 是
是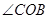 的平分线,求
的平分线,求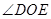 的度数.
的度数.
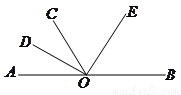
⑴一变:如图, ,
,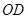 平分
平分 ,问
,问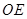 是否平分
是否平分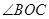 ?
?
⑵二变:如图,点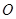 在直线
在直线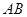 上,且
上,且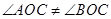 ,
,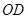 平分
平分 ,
, ,下面四个结论,错误的有( )
,下面四个结论,错误的有( )
①图中必有3个钝角; ②图中只有3对既相邻又互补的角;
③图中没有45°的角; ④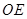 是
是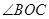 的平分线.
的平分线.
A.0个 B.1个 C.2个 D.3个
A
【解析】本题考查角平分线的性质、平角的定义、角与角之间的运算
根据OD是∠AOC的平分线,OE是∠COB的平分线,又知∠AOC+∠BOC=180°,故可得∠DOE的度数.
(1)由∠AOC+∠BOC=180°,∠DOE=90°,可得∠DOE= (∠AOC+∠BOC),进而得到∠COE=
(∠AOC+∠BOC),进而得到∠COE= ∠BOC.
∠BOC.
(2)根据∠AOC≠∠BOC,OD平分∠AOC,∠DOE=90°,再结合图形进行判断.
由题意可知∠DOC= ∠AOC,∠EOC=
∠AOC,∠EOC= ∠BOC.
∠BOC.
因为AB是一条直线,所以∠AOB=180°,也就是∠AOC+∠BOC=180°,∠DOE=∠DOC+∠EOC= ∠AOC+
∠AOC+
 ∠BOC=90°.
∠BOC=90°.
由题意可知 ,
, .
.
因为 是一条直线,所以
是一条直线,所以 ,也就是
,也就是 ,
,
 .
.
⑴解:因为 ,
, ,
,
所以
 ,
,
而 ,
, ,
,
所以 ,即
,即 平分
平分 .
.
(2)∵∠AOC≠∠BOC,OD平分∠AOC,∠DOE=90°,
∴图中必有3个钝角;图中只有3对既相邻又互补的角;图中没有45°的角;OE是∠BOC的平分线.
故选A.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:022
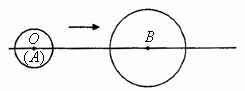
如图,![]() 从直线
从直线![]() 上的点
上的点![]() (圆心
(圆心![]() 与点
与点![]() 重合)出发,沿直线
重合)出发,沿直线![]() 以
以![]() 厘米/秒的速度向右运动(圆心
厘米/秒的速度向右运动(圆心![]() 始终在直线
始终在直线![]() 上).已知线段
上).已知线段![]() 厘米,
厘米,![]() ,
,![]() 的半径分别为
的半径分别为![]() 厘米和
厘米和![]() 厘米.当两圆相交时,
厘米.当两圆相交时,![]() 的运动时间
的运动时间![]() (秒)的取值范围是_____________.
(秒)的取值范围是_____________.
查看答案和解析>>
科目:初中数学 来源:2012年沪科版初中数学七年级上4.5角的大小比较练习卷(解析版) 题型:填空题
如图,点 是直线
是直线 上的点,
上的点, ,
, ,
, 三个角从小到大依次相差25°,则这三个角的度数是 .
三个角从小到大依次相差25°,则这三个角的度数是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,直线![]() :
:![]() 经过点
经过点![]() 一组抛物线的顶点
一组抛物线的顶点![]() (
(![]() 为正整数)依次是直线
为正整数)依次是直线![]() 上的点,这组抛物线与
上的点,这组抛物线与![]() 轴正半轴的交点依次是:
轴正半轴的交点依次是:![]() (
(![]() 为正整数),设
为正整数),设![]()
(1)求![]() 的值;
的值;
(2)求经过点![]() 的抛物线的解析式(用含
的抛物线的解析式(用含![]() 的代数式表示)
的代数式表示)
(3)定义:若抛物线的顶点与![]() 轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为:“美丽抛物线”.
轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为:“美丽抛物线”.
探究:当![]() 的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,请你求出相应的
的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,请你求出相应的![]() 的值.
的值.
 |
查看答案和解析>>
科目:初中数学 来源:浙江省模拟题 题型:填空题
 上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0)(n是正整数),设x1=a(0<a<1)。则当a=( )时,这组抛物线中存在美丽抛物线。
上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0)(n是正整数),设x1=a(0<a<1)。则当a=( )时,这组抛物线中存在美丽抛物线。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com