
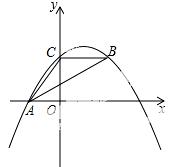
如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求 出点M的坐标;如果不存在,说明理由.
出点M的坐标;如果不存在,说明理由.
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
某班第一组12名同学在“爱心捐款”活动中,捐款情况统计如下表,则捐款数组成的一组数据中,中位数与众数分别是( )
| 捐款(元) | 10 | 15 | 20 | 50 |
| 人数 | 1 | 5 | 4 | 2 |
|
| A. | 15,15 | B. | 17.5,15 | C. | 20,20 | D. | 15,20 |
查看答案和解析>>
科目:初中数学 来源: 题型:
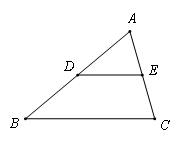
⑴证明三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半;
要求:根据图1写出定理的已 知、求证、证明;在证明过程中,至少有两外写
知、求证、证明;在证明过程中,至少有两外写 出推理的依据(“已知”除外)
出推理的依据(“已知”除外)
⑵如图2,在□ABCD中,对角线交点为O,A1、B1、C1、D1分别是OA、OB、OC、OD的中点,A2、B2、C2、D2分别是OA1、OB1、OC1、OD1的中点,…以此类推
 若在□ABCD的周长为1,直接用算式表示各四边形的周长之
若在□ABCD的周长为1,直接用算式表示各四边形的周长之 和l;
和l;
 ⑶借助图形3反映的规律,猜猜l可能是多少?
⑶借助图形3反映的规律,猜猜l可能是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
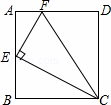
如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论:
①∠AEF=∠BCE;
②AF+BC>CF;
③S△CEF=S△EAF+S△CBE;
④若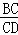 =
= ,则△CEF≌△CDF.
,则△CEF≌△CDF.
其中正确的结论是 .(填写所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com