
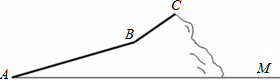
 数学活动小组组织一次登山活动,他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为200$\sqrt{13}$米,斜坡BC的长为200$\sqrt{2}$米,坡度是1:1,已知A点海拔121米,C点海拔721米.
数学活动小组组织一次登山活动,他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为200$\sqrt{13}$米,斜坡BC的长为200$\sqrt{2}$米,坡度是1:1,已知A点海拔121米,C点海拔721米.分析 (1)过C作CF⊥AM,F为垂足,过B点作BE⊥AM,BD⊥CF,E、D为垂足,根据斜坡BC的坡度是1:1,可得∠CBD=45°,继而可求得CD的长度,求出B点的高度;
(2)根据(1)中求得B点的高度,AB=200$\sqrt{13}$米,利用勾股定理求出AE的长度,易求得AB的坡度.
(3)根据CF⊥AM,BE⊥AM,BD⊥CF,得出四边形EFDB是矩形,继而可求得AF=800米,CF=600米,利用勾股定理即可求得AC的长度.
解答 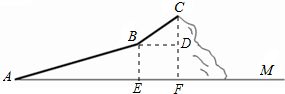 解:(1)如图,过C作CF⊥AM,F为垂足,过B点作BE⊥AM,BD⊥CF,E、D为垂足,
解:(1)如图,过C作CF⊥AM,F为垂足,过B点作BE⊥AM,BD⊥CF,E、D为垂足,
∵斜坡BC的坡度是1:1,
∴$\frac{CD}{BD}$=$\frac{1}{1}$,
∴CD=BD,
∴∠BCD=45°
∴在C点测得B点的俯角为45°,
∴∠CBD=45°,又BC=200$\sqrt{2}$米,
∴CD=200$\sqrt{2}$×sin45°=200$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=200(米),
∵A点海拔121米,C点海拔721米,
∴CF=721-121=600(米)
∴B点的铅直高度为600-200=400(米),
即斜坡B点处的高度为400米;
(2)∵BE=400米,
∴AB=200$\sqrt{13}$米,AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\sqrt{({200\sqrt{13})}^{2}-40{0}^{2}}$=600(米),
∴AB的坡度iAB=$\frac{BE}{AE}$=$\frac{400}{600}$=$\frac{2}{3}$,
故斜坡AB的坡度为1:1.5.
(3)∵CF⊥AM,BE⊥AM,BD⊥CF,
∴四边形EFDB是矩形,
∴EF=BD=200米,BE=DF=400米,
∴AF=200+600=800米,CF=CD+DF=200+400=600米,
∴AC=$\sqrt{A{F}^{2}+C{F}^{2}}$=1000米.
即钢缆AC的长度为1000米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据俯角构造直角三角形,要求同学们熟练掌握坡度的定义.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
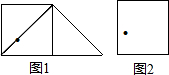 如图,正方形的对角线上有一个小孔,经过小孔剪一刀(不剪曲线和折线)可以将剪下的两片拼成一个三角形,拼成的三角形内部没有小孔,如图1;图2中的正方形中也有一个小孔,但它不在对角线上,将它剪成三片,用剪成的三片拼成一个三角形,要求拼成的三角形内部没有小孔.仿照图1把剪切线和拼成的三角形画出来.
如图,正方形的对角线上有一个小孔,经过小孔剪一刀(不剪曲线和折线)可以将剪下的两片拼成一个三角形,拼成的三角形内部没有小孔,如图1;图2中的正方形中也有一个小孔,但它不在对角线上,将它剪成三片,用剪成的三片拼成一个三角形,要求拼成的三角形内部没有小孔.仿照图1把剪切线和拼成的三角形画出来.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a-b)2=a2-b2 | B. | -x•(2x2+1)=-2x3+x | ||
| C. | (a+2b)2=a2+2ab+4b2 | D. | 2a•(-3a)=-6a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
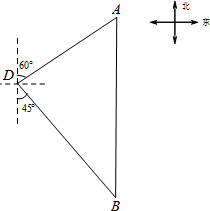 钓鱼岛自古以来就是中国的神圣领土,为宣誓主权,我海监船编队奉命在钓鱼岛附近海域进行维权活动.如图,一艘海监船位于钓鱼岛D的北偏东60°方向,与钓鱼岛的距离为16海里的A处,它沿正南方向航行,航行1小时后,发现此时海监船位于钓鱼岛的南偏东45°方向上的B处.
钓鱼岛自古以来就是中国的神圣领土,为宣誓主权,我海监船编队奉命在钓鱼岛附近海域进行维权活动.如图,一艘海监船位于钓鱼岛D的北偏东60°方向,与钓鱼岛的距离为16海里的A处,它沿正南方向航行,航行1小时后,发现此时海监船位于钓鱼岛的南偏东45°方向上的B处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com