练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    解方程：3x6-15=0．
    考点：立方根
    专题：
    分析：先移项，然后化未知数系数为1，最后开立方．
    解答：解：由原方程，得
    3x6=15，
    化系数为1，得
    x6=5，
    开立方，得
    x=
    35
    ．
    点评：此题主要考查了求一个数的立方根，解题时应先找出所要求的这个数是哪一个数的立方．由开立方和立方是互逆运算．注意一个数的立方根与原数的性质符号相同．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

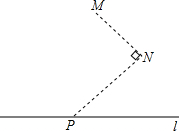    如图所示，在水渠l的同一侧有两个水池M与N，把水渠水先引到水池N，再由N引人水池M．连接MN，作∠MNP=90°，NP交l于点P，将水渠水由P放到N，再由N放到M，所行路径最短，对吗？如果不对，你是怎样设计的？写出你的设计方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    阅读下列材料：
    x+
    1
    x
    =c+
    1
    c
    的解是x1=c，x2=
    1
    c
    ；
    x-
    1
    x
    =c-
    1
    c
    的解是x1=c，x2=-
    1
    c
    ；
    x+
    2
    x
    =c+
    2
    c
    的解是x1=c，x2=
    2
    c
    ；
    x+
    3
    x
    =c+
    3
    c
    的解是x1=c，x2=
    3
    c
    ；
    …
    （1）请观察上述方程与解的特征，猜想方程x+
    m
    x
    =c+
    m
    c
    的解，并验证你的结论．
    （2）利用这个结论解关于x的方程：x+
    2
    x-1
    =a+
    2
    a-1
    ．

    查看答案和解析>>

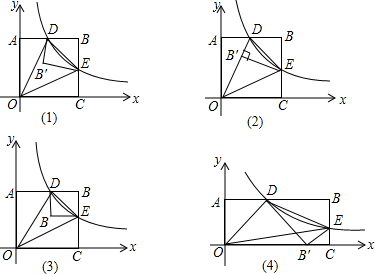
    科目：初中数学 来源： 题型：

    如图1，在平面直角坐标系中，A（0，n），C（m，0），双曲线y=
    12
    x
    （x＞0）与矩形OABC的两边AB、BC分别交于D、E两点，连接OD、OE、DE，将△DBE沿DE翻折后得△DB′E．
    探究一：如图2，若点D为AB中点时，点B′又恰好落在线段OD上，证明：OE平分∠DOC；
    探究二：如图3，若OE平分∠DOC，当四边形DB′EB是正方形时，求矩形OABC的面积；
    探究三：如图4，若点D在直线y=
    4
    3
    x上，是否存在m的值使B′点落在x轴上，若存在，求出点E的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某工厂用铝合金材料加工一批形状如图1所示的长方形窗框，窗框的内部安装透明玻璃．（铝合金材料的宽度都相同，接口用料忽略不计）

    （1）用含a的代数式表示制作一个该种窗框所需铝合金材料的总长度；
    （2）已知每根铝合金原材料的长为20a厘米，铝合金材料费100元/根，若要做50个如图1所示的铝合金窗框，至少需要铝合金材料费多少元？请说明怎样裁料；
    （3）图2是由两扇如图1所示的玻璃窗组装成且处于完全关闭状态的窗户，图3是由图2开窗通风时的示意图．
    ①求铝合金材料的宽度；（用含a的代数式表示）
    ②当a=20时，求完全打开玻璃窗时的最大通风面积．（精确到0.1平方厘米）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

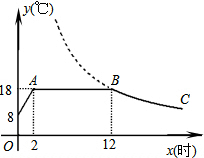    我市某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种，图是某天恒温系统从开启到关闭及关闭后，大棚内温度y（℃）随时间x（小时）变化的函数图象，其中BC段是双曲线y=
    k
    x
    的一部分．请根据图中信息解答下列问题：
    （1）恒温系统在这天保持大棚内温度18℃的时间有多少小时？
    （2）求k的值；
    （3）当x=16时，大棚内的温度约为多少度？
    （4）一天24小时大棚内温度超过12℃的时间有多少小时？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

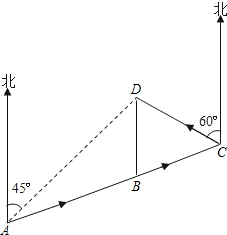    如图，要环绕A、B、C、D四地修筑一条高等级公路ABCDA．已知A、B、C三地在同一直线上，D地在A地的北偏东45°方向，在B地的正北方向，在C地北偏西60°方向，C地在A地的北偏东75°方向，B、D两地相距10km．如果该公路每公里造价为2000万元，求该公路全长的造价是多少万元？（用根号表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如果（2m+n）2+3（2m+n）-4=0，那么2m+n的值是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    化简：（
    1
    a
    +1）•
    1-a2
    1+2a+a2
    ．

    查看答案和解析>>

    同步练习册答案