
 甲、乙两车分别从相距200千米的A、B两地同时出发相向而行,甲到B地后立即返回A地,乙从B地直接到达A地,它们距A地的距离y(km)与行驶时间x(h)之间的函数图象如图所示.
甲、乙两车分别从相距200千米的A、B两地同时出发相向而行,甲到B地后立即返回A地,乙从B地直接到达A地,它们距A地的距离y(km)与行驶时间x(h)之间的函数图象如图所示.
|
|
|
|
|


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在①AB=CD;②AD=CB;③EF分别是AB、CD的中点;④DE=BF这四个命题,选取三个作为条件,能否得出下列结论,并说明理由.
如图,在①AB=CD;②AD=CB;③EF分别是AB、CD的中点;④DE=BF这四个命题,选取三个作为条件,能否得出下列结论,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
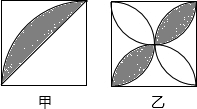 如图(甲)、(乙)是两个边长相等的正方形,甲图以边为半径在正方形内画圆弧,连接对角线;乙图以各边为直径在正方形内画半圆,阴影部分的面积分别记为S甲、S乙,那么S甲和S乙的大小关系是:S甲
如图(甲)、(乙)是两个边长相等的正方形,甲图以边为半径在正方形内画圆弧,连接对角线;乙图以各边为直径在正方形内画半圆,阴影部分的面积分别记为S甲、S乙,那么S甲和S乙的大小关系是:S甲查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| x+1 |
| 1 |
| x+5 |
| 1 |
| x+2 |
| 1 |
| x+4 |
| 6 |
| x2-25 |
| 3 |
| x2+8x+15 |
| 5 |
| x2-2x-15 |
| 1-x |
| x-2 |
| 1 |
| x-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com