
如图,在▱ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF,
(1)求证:四边形ABCD为矩形;
(2)过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4,求CG.

考点:
矩形的判定与性质;勾股定理;平行四边形的性质.
分析:
(1)求出∠BAE=90°,根据矩形的判定推出即可;
(2)求出△BGE面积,根据三角形面积公式求出BG,得出EG长度,根据勾股定理求出GH,求出BE,得出BC长度,即可求出答案.
解答:
(1)证明:∵F为BE中点,AF=BF,
∴AF=BF=EF,
∴∠BAF=∠ABF,∠FAE=∠AEF,
在△ABE中,∠BAF+∠ABF+∠FAE+∠AEF=180°,
∴∠BAF+∠FAE=90°,
又四边形ABCD为平行四边形,
∴四边形ABCD为矩形;

(2)解:连接EG,过点E作EH⊥BC,垂足为H,
∵F为BE的中点,FG⊥BE,
∴BG=GE,
∵S△BFG=5,CD=4,
∴S△BGE=10= BG•EH,
BG•EH,
∴BG=GE=5,
在Rt△EGH中,GH= =3,
=3,
在Rt△BEH中,BE= =4
=4 =BC,
=BC,
∴CG=BC﹣BG=4 ﹣5.
﹣5.
点评:
本题考查了矩形的判定,勾股定理,三角形的面积,线段垂直平分线性质等知识点的应用,主要考查学生综合运用性质进行推理的能力,题目比较好,有一定的难度.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
如图,∠1=∠2,∠C=∠B,下列结论中不正确的是( )
A. △DAB≌△DAC B. △DEA≌△DFA C. CD=DE D. ∠AED=∠AFD
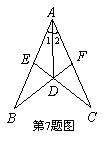
查看答案和解析>>
科目:初中数学 来源: 题型:
下列三角形中,是直角三角形的是( )
(A)三角形的三边满足关系a+b=c (B)三角形的三边比为1∶2∶3
(C)三角形的一边等于另一边的一半 (D)三角形的三边为9,40,41
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正方形ABCD的边长为2,点E、F分别为边AD、BC上的点,EF= ,点G、H分别为AB、CD边上的点,连接GH,若线段GH与EF的夹角为45°,则GH的长为( )
,点G、H分别为AB、CD边上的点,连接GH,若线段GH与EF的夹角为45°,则GH的长为( )

|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
如图是置于水平地面上的一个球形储油罐,小敏想测量它的半径.
 在阳光下,他测得球的影子的最远点A到球罐与地面接触点B的
在阳光下,他测得球的影子的最远点A到球罐与地面接触点B的
距离是10米(如示意图,AB=10米);同一时刻,他
又测得竖直立在地面上长为1米的竹竿的影子长为2
米,那么,球的半径是 米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com