
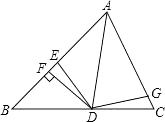
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为64和42,则△EDF的面积为 .
【答案】9
【解析】
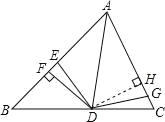
试题分析:过点D作DH⊥AC于H,根据角平分线上的点到角的两边距离相等可得DF=DH,再利用“HL”证明Rt△ADF和Rt△ADH全等,Rt△DEF和Rt△DGH全等,然后根据全等三角形的面积相等列方程求解即可.
如图,过点D作DH⊥AC于H, ∵AD是△ABC的角平分线,DF⊥AB, ∴DF=DH,
在Rt△ADF和Rt△ADH中,![]() , ∴Rt△ADF≌Rt△ADH(HL), ∴SRt△ADF=SRt△ADH,
, ∴Rt△ADF≌Rt△ADH(HL), ∴SRt△ADF=SRt△ADH,
在Rt△DEF和Rt△DGH中![]() ,, ∴Rt△DEF≌Rt△DGH(HL), ∴SRt△DEF=SRt△DGH,
,, ∴Rt△DEF≌Rt△DGH(HL), ∴SRt△DEF=SRt△DGH,
∵△ADG和△AED的面积分别为64和42, ∴42+SRt△DEF=64﹣SRt△DGH, ∴SRt△DEF=9.


科目:初中数学 来源: 题型:
【题目】下列哪组条件能够判定四边形 ABCD 是平行四边形?( )
A.AB // CD , AD BCB.AB CD , AD BC
C.A B , C DD.AB AD , CB CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE,且∠1=∠B=∠C.
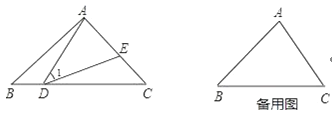
(1)由题设条件,请写出三个正确结论:(要求不再添加其他字母和辅助线,找结论过程中添加的字母和辅助线不能出现在结论中,不必证明)
答:结论一: ;
结论二: ;
结论三: .
(2)若∠B=45°,BC=2,当点D在BC上运动时(点D不与B、C重合),
①求CE的最大值;
②若△ADE是等腰三角形,求此时BD的长.
(注意:在第(2)的求解过程中,若有运用(1)中得出的结论,须加以证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级⑴班的座位共有6排8列,张军同学的座位在2排3列,我们可以记作(2,3),那么吴灏同学的座位在5排6列,应记作( )
A. (5,6) B. (6,5) C. (6,8) D. (3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区2015年屋顶绿化面积为2000平方米,计划2017年屋顶绿化面积要达到2880平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com