
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点D,E,F分别是边AB,BC,AC的中点,连接DE、DF,动点P,Q分别从点A、B同时出发,运动速度均为1cm/s,点P沿AFD的方向运动到点D停止;点Q沿BC的方向运动,当点P停止运动时,点Q也停止运动.在运动过程中,过点Q作BC的垂线交AB于点M,以点P,M,Q为顶点作平行四边形PMQN.设平行四边形边形PMQN与矩形FDEC重叠部分的面积为y(cm2)(这里规定线段是面积为0的几何图形),点P运动的时间为x(s)
(1)当点P运动到点F时,CQ= cm;
(2)在点P从点F运动到点D的过程中,某一时刻,点P落在MQ上,求此时BQ的长度;
(3)当点P在线段FD上运动时,求y与x之间的函数关系式.
(1)5。
(2) (cm)。
(cm)。
(3)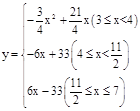 。
。
解析试题分析:(1)当点P运动到点F时,求出AF=FC=3cm,BQ=AF=3cm,即可求出答案。
(2)根据在点P从点F运动到点D的过程中,点P落在MQ上得出方程t+t﹣3=8,求出即可。
(3)求出DE= AC=3,DF=
AC=3,DF= BC=4,证△MBQ∽△ABC,求出MQ=
BC=4,证△MBQ∽△ABC,求出MQ=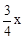 ,分为三种情况:①当3≤x<4时,重叠部分图形为平行四边形,根据y=PN•PD代入求出即可;②当4≤x<
,分为三种情况:①当3≤x<4时,重叠部分图形为平行四边形,根据y=PN•PD代入求出即可;②当4≤x< 时,重叠部分为矩形,根据图形得出
时,重叠部分为矩形,根据图形得出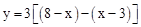 ;③当
;③当 ≤x≤7时,重叠部分图形为矩形,根据图形得出
≤x≤7时,重叠部分图形为矩形,根据图形得出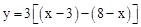 ,求出即可。
,求出即可。
解:(1)当点P运动到点F时,
∵F为AC的中点,AC=6cm,∴AF=FC=3cm。
∵P和Q的运动速度都是1cm/s,∴BQ=AF=3cm。
∴CQ=8cm﹣3cm=5cm。
(2)设在点P从点F运动到点D的过程中,点P落在MQ上,如图,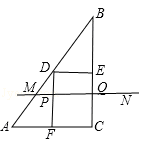
则t+t﹣3=8,∴t= 。
。
∴BQ的长度为 ×1=
×1= (cm)。
(cm)。
(3)∵D、E、F分别是AB、BC、AC的中点,
∴DE= AC=
AC= ×6=3,DF=
×6=3,DF= BC=
BC= ×8=4。
×8=4。
∵MQ⊥BC,∴∠BQM=∠C=90°。
∵∠QBM=∠CBA,∴△MBQ∽△ABC。
∴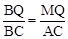 ,即
,即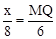 。∴MQ=
。∴MQ=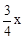 。
。
分为三种情况讨论:
①当3≤x<4时,重叠部分图形为平行四边形,如图,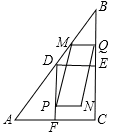
y=PN•PD=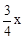 (7﹣x),
(7﹣x),
即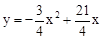 。
。
②当4≤x< 时,重叠部分为矩形,如图,
时,重叠部分为矩形,如图,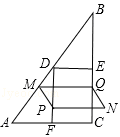
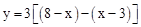 ,
,
即y=﹣6x+33。
③当 ≤x≤7时,重叠部分图形为矩形,如图,
≤x≤7时,重叠部分图形为矩形,如图,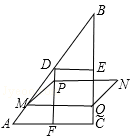
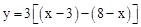 ,
,
即y=6x﹣33。
综上所述,当点P在线段FD上运动时, y与x之间的函数关系式为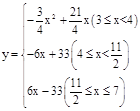 。
。


科目:初中数学 来源: 题型:
| A、16℃≤t≤18℃ | B、16℃≤t≤20℃ | C、16℃≤t≤22℃ | D、18℃≤t≤18℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
某初中学校共有学生720人,该校有关部门从全体学生中随机抽取了50人,对其到校方式进行调查,并将调查的结果制成了如图所示的条形统计图,由此可以估计全校坐公交车到校的学生有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
丁丁参加了一次智力竞赛,共回答了30道题,题目的评分标准是这样的:答对一题加5分,一题答错或不答倒扣1分.如果在这次竞赛中丁丁的得分要超过100分,那么他至少要答对多少题?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com